算法-动态规划(八)
概述
本文主要介绍树形 DP (简而言之,就是在树结构上完成 DP),与其相关的题目有:没有上司的舞会、树的最长路径、树的中心、皇宫看守。
没有上司的舞会
题目描述及示例
Ural 大学有 $N$ 名职员,编号为 $1~N$。他们的关系就像一棵以校长为根的树,父节点就是子节点的直接上司。每个职员有一个快乐指数,用整数 $Hi$ 给出,其中 $1 \leq i \leq N$。现在要召开一场周年庆宴会,不过,没有职员愿意和直接上司一起参会。在满足这个条件的前提下,主办方希望邀请一部分职员参会,使得所有参会职员的快乐指数总和最大,求这个最大值?
1 | Input: |
解题思路
数据存储
w[i]用于存储各职员的快乐指数,child[i][*]用于存储各职员的直接下级,root用于存储根职员。状态表示
对于树形 DP 而言,状态表示往往类似于:在以当前节点为根节点的子树中进行操作,所能得到的最大/最小价值。另外,本题中每个节点具有两种状态 —— 选或不选,则我们可以这样定义状态 $f[i][0]$:在以当前节点 $i$ 为根节点的子树中,选择职员参加舞会且当前节点所示职员不参加舞会情况下,所能得到的最大快乐指数,和 $f[i][1]$:在以当前节点 $i$ 为根节点的子树中,选择职员参加舞会且当前节点所示职员参加舞会情况下,所能得到的最大快乐指数。
状态转移
根据状态表示及题目描述,可很容易得到如下的状态转移方程:
当前节点所示职员参加舞会:
$$f[i][1] = \sum_{j = 1}^{child[j].length}(f[son][0]),(son = child[i][j])$$
当前节点所示职员不参加舞会:
$$f[i][0] = \sum_{j = 1}^{child[j].length}(max(f[son][0],f[son][1])),(son = child[i][j])$$
状态初始化
树形 DP 往往采用记忆化搜索实现,故而需要先将所有状态置为未知 (可使用状态值为 $-1$ 表示未知);搜索过程中,如果当前节点为叶节点,则设置 $f[i][0] = 0,f[i][1] = w[i]$ 即可。
执行记忆化搜索之时,需从根职员开始。
树的最长路径
题目描述及示例
给定一棵树,树中包含 $n$ 个结点(编号 $1 \sim n$)和 $n−1$ 条无向边,每条边都有一个权值 (权值非负)。现在请你找到树中的一条最长路径,换句话说,要找到一条路径,使得路径两个端点的距离最远。
1 | Input: |
解题思路
数据存储
child[i][*]用于存储各节点间关系,graph[i][k]用于存储节点间权值信息,root用于存储根节点。状态表示
根据题意:任意两点距离的最大值即为树的最长路径 (注意:该定义无视树边的有向性)。除使用基本的路径算法外,我们可以这样求取任意两个节点 $A,B$ 的距离:假定 $A,B$ 两点路径中最靠近树根的节点为 $C$,那么我们只需要求取节点 $C$ 到节点 $A,B$ 的距离,二者之和便是两节点的距离。这一求解方式是此题状态表示的基础,针对此题,我们可以这样定义状态 $f[i][0]$:当前节点到其子树节点的最大距离,和 $f[i][1]$:当前节点到其子树节点的次大距离。
当对所有节点求取两种状态后,树的最长路径值便是 $max(f[i][0] + f[i][1]),(0 \leq i < n)$。
状态转移
此题目的状态转移比较特殊,我们我们使用方程进行表述:
$$(f[i][0]) = maxFirst(0,f[j][0] + graph[i][j]),(0 \leq j < child[i].length)$$
$$(f[i][1]) = maxSecond(0,f[j][0] + graph[i][j]),(0 \leq j < child[i].length)$$
maxFirst表示最大值,maxSecond表示次大值。状态初始化
此题同样需要使用记忆化搜索加以实现。首先需要将所有状态置为未知 (可使用状态值为 $-1$ 表示未知);搜索过程中,如果当前节点为叶节点,则置 $f[i][0] = f[i][1] = 0$。
树的中心
题目描述及示例
给定一棵树,树中包含 $n$ 个结点(编号 $1~n$)和 $n−1$ 条无向边,每条边都有一个权值。请你在树中找到一个点,使得该点到树中其他结点的最远距离最近。
1 | Input: |
解题思路
数据存储
child[i][*]用于存储各节点间关系,graph[i][k]用于存储节点间权值信息,root用于存储根节点。状态表示
如果我们求得任意一点向下走和向上走所能到达树中其他节点的最远距离,那么此题便迎刃而解。我们首先简单看一个例子:
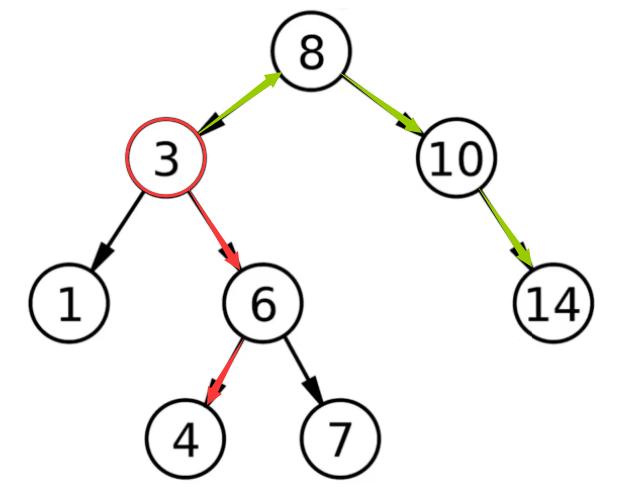
其中:我们求取节点 $3$ 向下走 (红线) 和向上走 (绿线) 所能达到树中其他节点的最远距离。
为求解向下走和向上走的最远距离,我们需要定义如下状态 $f[i][0]$:当前节点向下走所能走到的最远距离,$f[i][1]$:当前节点向下走所能走到的次远距离 (保存该值是有意义的,例子中节点 $3$ 向上走的最远距离就使用到节点 $8$ 的次远距离);$f[i][3]$:当前节点向上走所能走到的最远距离。另外我们需要保存当前节点向下走最远距离时所选择的节点及当前节点向下走次远距离时所选择的节点,分别使用 $p0[i]$ 和 $p1[i]$ 进行存储。
状态转移
$f[i][0]$ 和 $f[i][1]$ 的状态转移与上题一致,我们主要介绍 $f[i][3]$ 的状态转移。
对于状态 $f[i][3]$ 而言,它一定经由父节点的状态转移得到。如果当前节点非为父节点向下走最远路径时所选择节点,则当前状态应当由 $f[i][3]$ 或 $f[i][0]$ 转移得到;否则应当由 $f[i][3]$ 或 $f[i][1]$ 转移得到,故而其状态转移方程可表示如下:
$$f[i][3] = max(f[parent][3],f[i][0]) + graph[parent][i],(i \neq p0[parent])$$
$$f[i][3] = max(f[parent][3],f[i][1]) + graph[parent][i],(i = p0[parent])$$
实际实现中,我们会根据当前节点信息更新子节点状态,而非状态转移中根据父节点信息更新当前节点状态。
$f[i][0],f[i][1]$ 应当自底向上记忆化搜索,$f[i][3]$ 应当自顶向下搜索,且同时使用到状态 $f[i][0],f[i][1]$ ,故而此题应当分两次搜索,首先执行自底向上记忆化搜索,随后自顶向下搜索,以完成所有状态的更新。
状态初始化
如上所述,此题使用记忆化搜索实现 DP。首先需要将所有状态置为未知 (可使用状态值为 $-1$ 表示未知);当记忆化搜索 $f[i][0],f[i][1]$ 时,如果当前节点为叶节点,则置 $f[i][0] = f[i][1] = 0$;当搜索 $f[i][3]$ 时,我们直接置 $f[root][3] = 0$ 即可。
皇宫看守
题目描述及示例
太平王世子事件后,陆小凤成了皇上特聘的御前一品侍卫。皇宫各个宫殿的分布,呈一棵树的形状,宫殿可视为树中结点,两个宫殿之间如果存在道路直接相连,则该道路视为树中的一条边。已知,在一个宫殿镇守的守卫不仅能够观察到本宫殿的状况,还能观察到与该宫殿直接存在道路相连的其他宫殿的状况。
大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。可是陆小凤手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。帮助陆小凤布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。
1 | Input: |
解题思路
数据存储
child[i][*]用于存储各节点间关系,w[i]用于存储节点权值信息,root用于存储根节点。状态表示
题目要求每个结点都能够被看到,而且一个结点存在三种被看到的情况,故而我们可以这样定义状态 $f[i][0]$:当前子树的所有结点被看到、当前结点由父节点看到时,所需的最小代价,$f[i][1]$:当前子树的所有结点被看到、当前结点由子节点看到时,所需的最小代价,$f[i][2]$:当前子树的所有结点被看到、当前结点由自己看到时,所需的最小代价。
状态转移
对于 $f[i][0]$ 而言,当前节点已由父节点看到,那么子结点要么由自己看到,要么由其子结点看到;对于 $f[i][1]$ 而言,当前节点已由子结点看到,那么至少存在一个子结点需要由自己看到,其余子结点可选择由自己看到,也可选择由子节点看到;对于 $f[i][2]$ 而言,当前阶段已由自己看到,那么子结点要么由父节点看到,要么由自己看到,要么由子节点看到。
状态转移方程具体可表示如下:
$$f[i][0] = SUM,(SUM = \sum(min(f[j][1],f[j][2])),0 \leq j < child[i].length)$$
$$f[i][1] = min(SUM - min(f[j][1],f[j][2]) + f[j][2]),(0 \leq j < child[i].length)$$
$$f[i][2] = \sum(f[j][0],f[i][1],f[i][2]),(0 \leq < j < child[i].length)$$
状态初始化
本题同样使用记忆化搜索实现 DP。首先需要将所有状态置为未知 (可使用状态值为 $-1$ 表示未知);搜索过程中,如果当前结点为叶结点,则置 $f[i][0] = 0,f[i][1] = INF,f[i][2] = w[i]$ ($INF$ 表示无穷大)。