算法-动态规划(七)

发表于 分类于 ，
本文字数： 2.8k 阅读时长 ≈ 3 分钟

概述

本文主要介绍区间 DP，与其相关的题目有：石子合并、棋盘分割。

石子合并

题目描述及示例

设有 $N$ 堆石子排成一排，其编号为 $1，2，3，…，N$。每堆石子有一定的质量，可以用一个整数来描述，现在要将这 $N$ 堆石子合并成为一堆。每次只能合并相邻的两堆，合并的代价为这两堆石子的质量之和，合并后与这两堆石子相邻的石子将和新堆相邻，合并时由于选择的顺序不同，合并的总代价也不相同。

例如有 $4$ 堆石子分别为 $1 3 5 2$， 我们可以先合并 $1、2$ 堆，代价为 $4$，得到 $4 \ 5 \ 2$， 又合并 $1，2$ 堆，代价为 $9$，得到 $9 \ 2$ ，再合并得到 $11$，总代价为 $4+9+11=24$。如果第二步是先合并 $2，3$ 堆，则代价为 $7$，得到 $4 7$，最后一次合并代价为 $11$，总代价为 $4+7+11=22$。

问题是：找出一种合理的方法，使总的代价最小?

1
2
3
4
5
6
7
8
9
Input:
// 第一行包含一个数N，表示石子的堆数。
4
// 第二行包含N个数，表示每堆石子的质量。
1 3 5 2
    
Output:
// 输出一个整数，表示最小代价。
22

解题思路

  • 数据存储

    prefix[i] 用于存储石子质量的前缀和。

  • 状态表示

    我们直接这样表示状态 $f[i][j]$：合并区间 $[i,j]$ 所示石子，所需的最小代价。

  • 状态转移

    题目要求 “只有相邻石子才能合并”，故而当前状态 $f[i][j]$ 一定是由 $f[i][k]$ 和 $f[k + 1][j]$ 转移得到。由于并不知道具体 $k$ 取值，故而需要枚举区间内所有合法 $k$ 值。

    状态转移方程具体如下：

    $$f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + prefix[j] - prefix[i - 1]),(i \leq k < j)$$

  • 状态初始化

    题意要求求取最小值，故而首先将全部状态初始化为无穷大，随后指定 $f[i][i] = 0,(0 \leq i \leq N)$。

对于区间 DP 问题，使用记忆化搜索实现比较简单；使用递推实现则比较麻烦，但是它具有一定模板，我们在此列出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 状态表示(N*N矩阵)。
int[][] f;

// 首先枚举步长，随后枚举起点。
for (int i = 1; i < N; i++) {
    for (int j = 0; j + i < N; j++) {
        // 获取区间左右端点。
        int L = j, R = j + i;
        // 枚举区间中间点，实现状态转移。
        for (int k = j; k < R; k++) {
            f[L][R] = transfer(f[L][k],f[k + 1][R]);
        }
    }
}

此题有一个十分重要的变体 —— 环形石子合并，即当石子环形放置时，如何合并才能使得代价最小。

我们可以枚举所有断点，从而将环形石子合并问题转换为 $N$ 个石子合并问题 (根据上面代码，可以知道其时间复杂度为 $O(N^3)$)，最终寻找 $N$ 个石子合并问题的最小代价即可。容易得知：这种方法的时间复杂度为 $O(N^4)$。

上面这种方法的时间复杂度偏高，另有一种取巧的方法可以大大降低时间复杂度：复制 $N$ 个石子并将它们按序排列在原先 $N$ 个石子序列之后，从而形成长度为 $2N$ 的石子序列 (举例：对于例题而言，形成的石子序列便是 1 3 5 2 1 3 5 2)。对此序列执行区间 DP 并寻找 $f[i,i + N],(0 \leq i < N)$ 的最小值作为环形石子合并的最小代价即可。容易得知：此种方法的时间复杂度为 $(2N)^2 = 8N^2$。

棋盘分割

题目描述及示例

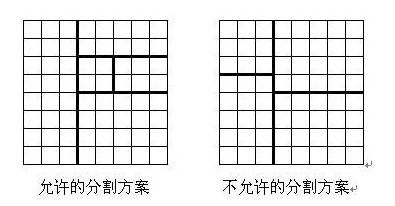
将一个 $8 \times 8$ 的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了 $(n-1)$ 次后，连同最后剩下的矩形棋盘共有 $n$ 块矩形棋盘 (每次切割都只能沿着棋盘格子的边进行)。

原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成 $n$ 块矩形棋盘，并使各矩形棋盘总分的均方差最小 (均方差：$\sigma = \sqrt{\sum_{i = 1}^n(x_i - \overline{x})^2/n}$，其中 $x_i$ 为各棋盘分值，$\overline{x}$ 为各棋盘分值的平均值)。

请编程对给出的棋盘及n，求出均方差的最小值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Input:
// 第一行包含一个整数n。
3
// 接下来8行，每行8个整数，表示棋盘各位置的分值。
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

Output:
// 输出一个浮点数，表示最小均方差值。
1.633

解题思路

  • 数据存储

    我们可以先行求取 $n \times \sigma^2$ 的最小值，随后一步转换便得到题目要求的均方差最小值。在求取 $n \times \sigma^2$ 时，我们需要动态获取棋盘分值，故而使用 prefix[i][j] 存储二维前缀和，随后基于此可一步求得指定棋盘分值。另外，我们需要获取各棋盘分值的平均值，此可通过 $prefix[7][7] / 8$ 求得。

  • 状态表示

    此题属于区间 DP 的二维扩展，另外题目涉及分割次数，故而我们直接给出状态表示 $f[x1][y1][x2][y2][k]$：将 $(x1,y1) \sim (x2,y2)$ 所示矩形区间分割 $k$ 次，所需的最小代价 (具体指代 $(x_i - \overline{x})^2$)。

  • 状态转移

    根据题目而言，可以采取横向分割，也可采取纵向分割，故而状态转移方程可具体表示如下：

    横向切割：

    $$f[x1][y1][x2][y2][k] = min(f[x1][y1][x2][y2][k], f[x1][y1][t][y2][k - 1] + sum(x1,y1,t,y2),f[t + 1][y1][x2][y2][k - 1] + sum(t + 1,y1,x2,y2)),(x1 \leq t < x2)$$

    纵向切割：

    $$f[x1][y1][x2][y2][k] = min(f[x1][y1][x2][y2][k],f[x1][y1][x2][t][k - 1] + sum(x1,y1,x2,k),f[x1][k + 1][x2][y2][k - 1] + sum(x1,k + 1,x2,y2)),(y1 \leq t < y2)$$

    sum(x1,y1,x2,y2) 使用二维前缀和求取矩形区间内元素之和，具体返回值为 prefix[x2][y2] - prefix[x1 - 1][y2] - prefix[x2][y1 - 1] + prefix[x1 - 1][y1 - 1]。

  • 状态初始化

    这道题目没有办法使用递推，因为没有可用的初始化状态，故而应当使用记忆化搜索实现 DP。所有状态最初全部设为未知 (可使用状态值为 $-1$ 表示未知)；搜索过程中，如果无法继续分割，直接计算相关值即可。