算法-动态规划(六)

概述

本文主要介绍状态压缩 DP，与其相关的题目有：玉米地、炮兵阵地、最短 Hamilton 路径、开宝箱。

状态压缩 DP 属于一种比较另类的动态规划，类似于暴力破解，常用于 NP 问题的小规模求解。其核心在于使用二进制表示集合状态，故而我们需要简单介绍基于二进制的集合。

对于 int 整形而言，它由 $32$ 个 $bit$ 位组成。每个 $bit$ 位存在两种取值，故而每个 $bit$ 位可以表示两种状态，这刚好可以表示集合中元素是否存在。故而我们可以基于整数表示集合中元素状态。举例而言：假定存在五个依序而放的坑位，每个坑位可以种胡萝卜，也可不种胡萝卜，如何表示其所有状态？我们使用五个 $bit$ 位表示五个坑位，如果 $bit$ 位取值为 $1$，表示此坑位种胡萝卜；否则表示此坑位不种胡萝卜。那么区间 $[0,2^5 - 1]$ 中每个整数都映射为一个集合状态，共计 $2^5$ 种状态。

接下来我们简单介绍一些位操作：

• &​

  当使用二进制表示集合时，它可用于求取两个集合的交集。

• |

  当使用二进制表示集合时，它可用于求取两个集合的并集。

• ~

  当使用二进制表示集合时，它可用于求取一个集合的补集。

• ^

  当使用二进制表示集合时，它可用于求取两个集合的对称差。

• x | (1 << (i - 1))

  将数字 $x$ 的第 $i$ 位置为 $1$。

• x & (x - 1)

  将数字 $x$ 的最低位 $1$ 变为 $0$。

• x & -x

  将除最低位 $1$ 外的其余 $1$ 变为 $0$ (也就是树状数组中的 $lowBit$ 操作)。

状态压缩 DP 主要分为两种题型 —— 棋盘式、集合式。玉米地、炮兵阵地属于棋盘式题目，最短 Hamilton 路径、开宝箱属于集合式题目。棋盘式题目往往存在套路可用，而集合式题目则需随机应变 (换言之，就是难)。

玉米地

题目描述及示例

一块土地 $ m \times n $ 个小方格组成，现在要在土地中种植玉米。部分土地是不育的，无法种植；而且相邻的土地不能同时种植玉米，也就是种植玉米的所有方格之间都不会有公共边缘。现在给定土地的大小，请你求出有多少种种植方法。土地上什么都不种也算是一种方法。

// 数据范围：0 <= n,m <= 12。
Input:
// 第一行包含两个整数M和N，用于表示土地长宽。
2 3 
// 接下来包含M行，每行包含N个整数，表示当前方格是否贫瘠(1表示土地肥沃，0表示土地贫瘠)。
1 1 1
0 1 0
    
Output:
// 输出一个整数，表示种植方法树。
9

解题思路

• 数据存储

  g[i] 用于存储每行方格状态，如果该方格所代表土地肥沃，则置相应位为 $0$；否则置相应位为 $1$。对于例子而言，$g[0] = 0b000 = 0,g[1] = 0b101 = 5$。state[i] 用于存储可用状态。

• 状态表示

  对于这道题目而言，我们可以看到数据范围十分小，那么基本上可以确定它需要使用状态压缩 DP 进行解决。对于棋盘式题目，我们通常这样定义状态 $f[i][b]$：第 $i$ 行处于 $b$ 所示集合状态时，种植玉米的方案数。

• 状态转移

  进行状态转移之前，我们需要确定哪些集合状态可用。按照题目所言，横向相邻方格无法同时种植玉米，那么 $0b1001$ 这种状态是可用的，而 $0b110$ 这种状态是不可用的。我们需要从全体状态中选择所有可用状态至 state[i] 之中。

  由于纵向相邻方格也无法同时种植玉米，而且当前行状态仅与上一行状态相关，故而我们应当先行循环遍历上一行状态 (记为 $a$)，随后遍历当前行状态 (记为 $b$)，如果两者不相容，则当前状态 $b$ 无效，否则使用如下状态转移方程进行更新：

  $$f[i][b] = f[i][b] + f[i - 1][a],(a与b相容,b与g[i]相容)$$

  这里探讨两个问题：如何判断状态 $a$ 与 $b$ 是否相容？如何判断状态 $b$ 与 $g[i]$ 是否相容？

  首先回答第一个问题：$state[i]$ 中状态均满足“横向相邻方格无法同时种植玉米” 条件，现在需要判断满足 “纵向相邻方格也无法同时种植玉米” 这一条件。如果纵向相邻方格存在同时种植玉米，则相应位一定为 $1$，对状态 $a$、$b$ 执行与操作，其结果一定大于零。所以我们通过 a & b > 0 判断状态 $a$、$b$ 是否相容。

  接下来回答第二个问题：正如上面给定的 $g[i]$ 定义，如果 g[i] & b > 0，则贫瘠土地中种有玉米，不符合种植要求。故而使用此式可判断状态 $b$ 与 $g[i]$ 是否相容。

  提前将可用状态放置在 $state[i]$ 之中，意在减小搜索量。

• 状态初始化

  为简化初始化操作，我们使用 $g[1]$ 存放第 $0$ 行状态，依次而行，使用 $g[m + 1]$ 存放第 $m$ 行状态，此时状态维度便是 $(m + 1) \times state.length$。这样我们只需初始化 $f[0][state] = 0,(0 \leq state < state.length)$ 即可。

棋盘式状态压缩 DP 解题代码往往具有一定程式，我们在此举一模板：

// 状态表示存储(默认全部设为某值)。
int[][] f;
// 可用状态存储.
int[] state;

// 初始化相关状态。
for (int i = 0; i < f[0].length; i++) {
    f[0][i] = 0;
}

// 状态转移（首先枚举行，随后枚举上一行状态，最后枚举当前行状态）。
for (int i = 1; i < f.length; i++) {
    for (int a = 0; a < state.length; a++) {
        for (int b = 0; b < state.length; b++) {
			if (b 有效 && a与b相容) {
                f[i][b] = transfer(f[i][a]);
            }
        }
    }
}

// 得到题目答案。
return f[*][*];

炮兵阵地

题目描述及示例

司令部的将军们打算在 $N \times M$ 的网格地图上部署他们的炮兵部队。一个 $N \times M$的地图由 $N$ 行 $M$ 列组成，地图的每一格可能是山地 (用“H” 表示)，也可能是平原 (用“P”表示)，如下图所示。在每一格平原地形上最多可以布置一支炮兵部队 (山地上不能够部署炮兵部队)；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

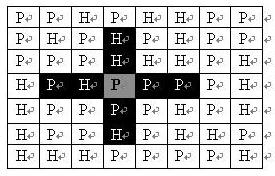
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。现在，将军们规划如何部署炮兵部队，在防止误伤的前提下 (保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内)，在整个地图区域内最多能够摆放多少我军的炮兵部队?

// 数据范围：0 <= n <= 100，0 <= m <= 10。
Input:
// 第一行包含两个正整数，分别表示N和M。
5 4
// 接下来N行，每一行含有连续的M个字符('P'或者'H')，表示地图具体情况。
PHPP
PPHH
PPPP
PHPP
PHHP
    
Output:
// 输出一个整数，表示最多能摆放的炮兵部队的数量。
6

解题思路

• 数据存储

  g[i] 用于存储每行方格状态，如果该方格可以放置炮兵，则置相应位为 $0$；否则置相应位为 $1$。对于例子而言，$g[0] = 0b0010 = 2,g[1] = 0b1100 = 12$。state[i] 用于存储可用状态，$cnt[i]$ 用于存储各可用状态中 $1$ 的个数。

• 状态表示

  与上题基本一致，数据范围比较小，可以使用状态压缩 DP 加以解决。由于当前行状态与前两行状态均有关，故而我们这样表示状态 $f[i][a][b]$：第 $i$ 行处于 $b$ 所示集合状态，且第 $i - 1$ 行处于 $a$ 所示集合状态时，能够摆放的最多炮兵部队数量。

• 状态转移

  我们首先确定哪些状态可用。按照题目所言，横向炮兵之间最少间隔两个方格，那么 $0b1001$ 这种状态是可用的，而 $0b0101$ 这种状态是不可用的。我们需要从全体状态中选择所有可用状态至 state[i] 之中，并计算相应的 $cnt[i]$。

  由于当前状态与前两行状态均有关，并且纵向炮兵之间最少间隔两个方格，故而我们应当先行循环遍历倒数第二行状态 (记为 $c$)，随后遍历倒数第一行状态 (记为 $a$)，最后遍历当前行状态 (记为 $b$)，如果三者状态不相容，则当前状态 $b$ 无效，否则使用如下状态转移方程进行更新：

  $$f[i][a][b] = max(f[i][a][b],f[i - 1][c][a] + cnt[i]),(a与g[i - 1]相容,b与g[i]相容，a,b,c之间相容)$$

  状态 $a$ 与 $g[i - 1]$、状态 $b$ 与 $g[i]$ 是否相容，与上题判断方法相同。我们使用 a & g[i - 1] > 0、b & g[i] > 0 进行判断即可。

  状态 $a$、$b$、$c$ 之间是否相容，需要判断各状态相同位置是否同时放置炮兵，那么我们可以使用等式 (a & b) | (b & c) | (a & c) > 0 进行判断。

• 状态初始化

  为简化初始化操作，我们使用 $g[1]$ 存放第 $0$ 行状态，依次而行，使用 $g[n + 1]$ 存放第 $n$ 行状态，此时状态维度便是 $(n + 1) \times state.length$。此时我们直接将所有状态初始化为 $0$ 即可。

最短 Hamilton 路径

题目描述及示例

给定一张 $N$ 个点的带权无向图，点从 $0 \sim N-1$ 标号，求起点 $0$ 到终点 $N-1$ 的最短Hamilton路径。 Hamilton路径的定义是从 $0$ 到 $N-1$ 不重不漏地经过每个点恰好一次。

// 数据范围：1 <= N <= 20。
Input:
// 第一行输入整数N。
5
// 接下来N行,每行N个整数，其中第i行第j个整数表示点i到j的距离。
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
    
Output:
// 输出一个整数，表示最短Hamilton路径的长度。
18

解题思路

• 数据存储

  graph[i][j] 用于存储图信息。

• 状态表示

  这道题目同样是数据范围比较小，另外求取最短 Hamilton 路径属于 NP 问题，因而可以使用状态压缩 DP 进行求解。

  题意需要获取从 $0$ 到 $N$ 的最短 Hamilton 路径，

  此题属于集合式题目，状态表示一般没有定式。我们在此直接给出状态表示 $f[i][state]$：从起点 $0$ 开始，依次经过 $state$ 状态所示点 (如果经过该点，则置相应位为1)，最终到达 $i$ ，所需的最短路径长度。

• 状态转移

  状态表示已经完成，状态转移就比较好理解：对于任意点 $k$ 而言，如果 $graph[k][i] != INF$，则我们由状态 $f[i][state - (1 << (i - 1))]$ 转移到 $f[i][state]$。

  状态转移方程具体表示如下：

  $$f[i][state] = min(f[i][state],f[k][state - (1 << (i - 1)) + graph[k][i]]),(0 \leq k < graph.length \ 且 \ i \neq k)$$

  注意：state 状态的第 $i$、$k$ 位均需为 1；考虑到状态转移所使用到的状态，我们应当先行循环 state，随后循环 $i$ (如果觉得别扭，可以将状态表示改为 $f[state][i]$)。

• 状态初始化

  题意要求求取最小值，故而首先全部初始化为无穷大，随后指定 $f[0][1] = 0$ 即可。

开宝箱

题目描述及示例

我们有 $N$ 个上锁的藏宝箱，编号依次为 $1 \sim N$。现有一家商店售卖 $M$ 把钥匙，第 $i$ 把钥匙售价为 $a_i$ 元，并且它可以解锁 $b_i$ 个宝箱 (对应编号为 $c_{i1} \sim c_{ib_i}$ )。请问打开所有箱子，最少需要多少钱？

// 数据范围：1 <= N <= 12,1 <= M <= 1000。
Input:
// 第一行包含两个整数，分别表示N和M。
2 3
// 接下来包含M组数据，每组数据由两行组成，第一行包含两个整数，表示钥匙价格及解锁宝箱数，第二行包含一系列数，表示可以解锁的宝箱编号。
10 1
1
15 1
2
30 2
1 2
    
Output:
// 输出一个整数，表示所需最少的钱。
25

解题思路

• 数据存储

  price[i] 用于存储第 $i$ 把钥匙价格，g[i] 用于存储第 $i$ 把钥匙所能打开的宝箱 (使用二进制进行存储)，corr[i][*] 用于存储能够开启第 $i$ 个宝箱的钥匙集合。

• 状态表示

  $N$ 的数据范围比较小，那么可以考虑使用状态压缩 DP 进行解决。此为集合式题目，我们直接给出状态表示 $f[state]$：打开 $state$ 所示宝箱，所需的最少钱。

• 状态转移

  以往状态转移都是根据已计算状态求解当前状态，这里我们采用另外一种状态转移方式：根据当前状态逐步求解未知状态。

  为处理状态转移，我们需要遍历 $f[state]$ 并求解它。假定我们遍历到 $f[t]$ 且 $f[t]$ 已求解得到，随后我们找到第一个尚未被解开的宝箱，根据 corr[i][*] 执行如下状态转移：

  $$f[t | g[key]] = min(f[t | g[key]],f[t] + price[key]),(key = corr[i][j],0 \leq j < corr[i].length)$$

• 状态初始化

  根据状态定义，首先全部初始化为无穷大，随后我们执行如下初始化：$f[0] = 0$。

对于此题而言，我们还可这样定义状态 $f[i][state]$：使用前 $i$ 把钥匙，打开 $state$ 所示宝箱，所需的最少钱。

那此时状态转移就略微麻烦：如果不使用当前钥匙，则 $f[i][state] = min(f[[i][state],f[i - 1][state]])$；如果使用当前钥匙，则 $f[i][state | key[i]] = min(f[i][state | key[i]], f[i][state] + price[i])$。