算法-动态规划(五)
概述
本文主要介绍状态机 DP,与其相关的题目有:大盗阿福、小 Q 假期、买卖股票的最佳时机 IV、最佳买卖股票时机含冷冻期。
对于一些动态规划题目而言,它们在某个时刻的状态仅涉及一个抉择 (例如:最长上升子序列,直接选择当前数字);而对于另外一些动态规划题目而言,它们在某个时刻的状态可能涉及多个抉择 (例如:01 背包,某个时刻可选择当前物品或者不选择当前物品;小 Q 假期,一天之内存在休息、工作、健身三种选择),此时就需要使用状态机 DP 进行处理,它可以很好地展现状态间转移情况,同时易于理解。
状态机 DP 借助于有限状态自动机构建状态,并据此进行状态转移,从而实现动态规划。
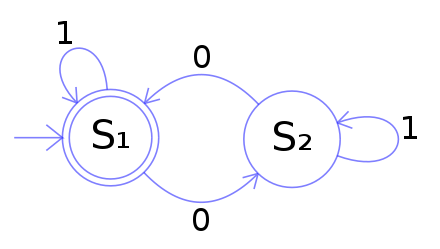
如果所涉抉择数目为 2,可以选择使用普通 DP 进行处理,也可以选择使用状态机 DP 进行处理。
大盗阿福
题目描述及示例
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。这条街上一共有 $N$ 家店铺,每家店中都有一些现金。阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。作为一向谨慎作案的大盗,阿福不愿意冒着被警察追捕的风险行窃。他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金?
1 | Input: |
解题思路
我们先使用普通 DP 解决此问题。
数据存储
money[i]用于存储各店铺现金数量。状态表示
既然数据是一维的,状态表示大概率也是一维的。我们可以这样定义状态 $f[i]$:在不惊动警察情况下,从前 $i$ 家店铺抢劫,所能得到的最下现金数量。
状态转移
这道题目的难点在于:如何保证不会同时洗劫两家相邻的店铺?对于状态 $f[i]$ 而言,如果选择洗劫当前店铺,则其只能从状态 $f[i - 2]$ 转移得到;否则从状态 $f[i - 1]$ 转移得到。故而状态转移方程可表示如下:
$$f[i] = max(f[i - 1], f[i - 2] + money[i]),(2 \leq i < money.length)$$
状态初始化
根据状态表示,我们可以这样初始化:指定 $f[0] = 0$。
接下来我们使用状态机 DP 解决此问题。
数据存储
money[i]用于存储各店铺现金数量。状态表示
对于店铺而言,它具有两种选择:被阿福抢劫和不被阿福抢劫。故而我们可以这样定义状态 $f[i][0]$:在不惊动警察情况下,抢劫以往店铺并且不抢劫当前店铺,所能得到的最下现金数量,和 $f[i][1]$:在不惊动警察情况下,抢劫以往店铺并且抢劫当前店铺,所能得到的最下现金数量。
状态转移
根据上述状态表示及 “无法同时抢劫相邻两家店铺” 要求,我们可以得到如下状态转移图:
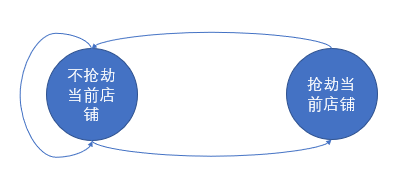
故而状态转移方程可表示如下:
$$f[i][0] = max(f[i - 1][0], f[i - 1][1])$$
$$f[i][1] = f[i - 1][0] + money[i]$$
状态初始化
根据状态表示,我们可以这样初始化:指定 $f[0][0] = 0,f[0][1] = money[0]$。
小 Q 假期
题目描述及示例
由于业绩优秀,公司给小 Q 放了 $N$ 天的假,身为工作狂的小 Q 打算在假期中工作、锻炼或者休息。他有个奇怪的习惯:不会连续两天工作或锻炼。只有当公司营业时,小 Q 才能去工作,只有当健身房营业时,小 Q 才能去健身,小 Q 一天只能干一件事。现给出假期中公司,健身房的营业情况,求小 Q 最少需要休息几天?
1 | Input: |
解题思路
数据存储
company[i]用于存储公司营业信息,gym[i]用于存储健身房营业信息。状态表示
对于任意一天,小 Q 具有三种选择 —— 休息、健身、工作。故而我们可以这样定义状态 $f[i][0]$:当天选择休息时,累计的最小休息天数,$f[i][1]$:当天选择健身时,累计的最小休息天数,$f[i][2]$:当天选择工作时,累计的最小休息天数。
状态转移
根据上述状态表示及 “不会连续两天工作或锻炼” 要求,我们可以得到如下状态转移图:
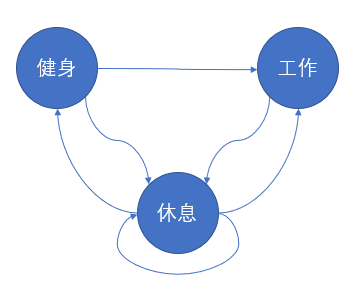
故而状态转移方程可表示如下:
$$f[i][0] = min(f[i - 1][0],f[i - 1][1],f[i - 1][2]) + 1$$
$$f[i][1] = min(f[i - 1][0],f[i - 1][2])$$
$$f[i][2] = min(f[i - 1][0],f[i - 1][1])$$
只有当天允许健身或工作,才会有状态 $f[i][1]$、$f[i][2]$ 的转移,否则该状态非法。
状态初始化
因为存储非法状态且需要求取最小值,故而我们首先将所有状态初始化为无穷大,随后指定合法初始状态:$f[0][0] = 1,f[0][1] = 0(if \ gym[i] = 1),f[0][2] = 0(if \ company[i]=1)$。
买卖股票的最佳时机 IV
题目描述及示例
给定一个数组,它的第 $i$ 个元素是一支给定的股票在第 $i$ 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成 $K$ 笔交易。注意: 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
1 | Input: |
解题思路
数据存储
price[i]用于存储股票价格。状态表示
对于任意一天,”我” 具有两种状态:手中有股票和手中无股票。那么我们可以这样定义状态 $f[i][0]$:第 $i$ 天手中没有股票,所能获取的最大利益,和 $f[i][1]$:第 $i$ 天手中有股票,所能获取的最大利益。
另外,对于本题目而言,它考虑交易次数,故而我们这样定义状态 $f[i][0][k]$:第 $i$ 天手中没有股票,且处于第 $k$ 次交易已经完成时,所能获取的最大利益;和 $f[i][1][k]$:第 $i$ 天手中有股票,且正处于第 $k$ 次交易时,所能获取的最大利益。
买入股票即看作一次交易的开始。
状态转移
根据上述状态表示,我们可以得到如下状态转移图:
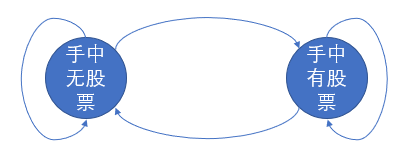
故而状态转移方程可表示如下:
$$f[i][0][k] = max(f[i - 1][0][k],f[i - 1][1][k] + price[i])$$
$$f[i][1][k] = max(f[i - 1][1][k],f[i - 1][0][k - 1] - price[i])$$
状态初始化
为求取状态最大值,首先将所有状态初始化为无穷小。由于状态表示为第 $i$ 天,故而需要这样初始化:指定 $f[0][0][k] = 0(0 \leq k \leq K),f[0][1][1] = -price[0]$。
最佳买卖股票时机含冷冻期
题目描述及示例
给定一个长度为 $N$ 的数组,数组中的第 $i$ 个数字表示一个给定股票在第 $i$ 天的价格。设计一个算法计算出最大利润,在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票)。你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。卖出股票后,你无法在第二天买入股票 (即冷冻期为 $1$ 天)。
1 | Input: |
解题思路
数据存储
price[i]用于存储股票价格。状态表示
相比上一道题目,”我” 具有三种状态:手中有股票、手中无股票的第一天、手中无股票的第 $i \geq 2$ 天。 那么我们可以这样定义状态 $f[i][0]$:第 $i$ 天且手中有股票,所能获取的最大利益,$f[i][1]$:第 $i$ 天且手中无股票的第一天,所能获取的最大利益,$f[i][2]$:第 $i$ 天且手中无股票的第 $i \geq 2$ 天,所能获取的最大利益。
状态转移
根据上述状态表示及 “冷冻期” 要求,我们可以得到如下状态转移图:
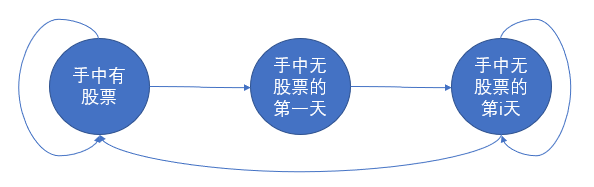
故而状态转移方程可表示如下:
$$f[i][0] = max(f[i - 1][0],f[i - 1][2] - price[i])$$
$$f[i][1] = f[i - 1][0] + price[i]$$
$$f[i][2] = max(f[i - 1][2],f[i - 1][1])$$
状态初始化
为求取状态最大值,首先将所有状态初始化为无穷小。由于状态表示为第 $i$ 天,故而需要这样初始化:指定 $f[0][0] = -price[i],f[0][2] = 0$。