算法-动态规划(四)
概述
本文主要介绍背包 DP,与其相关的题目有:01 背包、完全背包、多重背包、混合背包、二维费用的背包、分组背包、有依赖的背包。
01 背包
题目描述及示例
有 $N$ 件物品和一个容量是 $V$ 的背包。每件物品只能使用一次。第 $i$ 件物品的体积是 $v_i$,价值是 $w_i$。求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大?
1 | Input: |
解题思路
数据存储
v[i]用于存储各物品体积,w[i]用于存储各物品价值。状态表示
对于背包问题而言,状态表示往往都是二维的。我们可以这样表示状态 $f[i][j]$:从前 $i$ 个物品中选择,并将它们装入容量为 $j$ 的背包中,所能得到的最大价值。
状态转移
对于状态 $f[i][j]$ 而言,如果它选择当前物品 $i$,则其应当由状态 $f[i - 1][j - v[i]]$ 转移得到;否则应当由状态 $f[i - 1][j]$ 转移得到。故而状态转移方程可表示如下:
$$f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]),(j \geq v[i])$$
观察状态转移方程,可以发现:状态 $f[i][\ast]$ 的转移仅涉及 $f[i - 1][\ast]$。故而实现之中,我们可以使用滚动数组以优化空间。更进一步,我们发现:状态 $f[i][j]$ 仅从状态 $f[i - 1][k],(k < j)$ 转移得到,故而我们可从后往前更新一维数组以达到滚动数组的效果 (此时状态表示优化为 $f[j]$,表示将物品装入容量为 $j$ 的背包中所能得到的最大价值)。
状态初始化
根据状态表示,我们可这样初始化:指定 $f[0][j] = 0,(0 \leq j \leq V)$。
完全背包
题目描述及示例
有 $N$ 种物品和一个容量是 $V$ 的背包,每种物品都有无限件可用。第 $i$ 种物品的体积是 $v_i$,价值是 $w_i$。求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大?
1 | Input: |
解题思路
数据存储
v[i]用于存储各物品体积,w[i]用于存储各物品价值。状态表示
与 01 背包 状态表示相同,我们可以这样表示状态 $f[i][j]$:从前 $i$ 个物品中选择,并将它们转入容量为 $j$ 的背包中,所能得到的最大价值。
状态转移
由于物品可无限次选用,故而对于状态 $f[i][j]$ 而言,如果它不选择当前物品 $i$,则应当由状态 $f[i - 1][j]$ 转移得到;如果它选择一个当前物品 $i$,则应当由状态 $f[i - 1][j - v[i]]$ 转移得到;如果它选择 $k$ 个当前物品 $i$,则应当由状态 $f[i - 1][j - k \times v[i]]$ 转移得到。
状态转移方程具体表示如下:
$$f[i][j] = max(f[i - 1][j],f[i - 1][j - v[i]] + w[i],\dots,f[i - 1][j - k \times v[i]] + k \times w[i]),(j \geq k*w[i])$$
对于状态 $f[i][j - v[i]]$ 而言,其状态转移方程具体为:
$$f[i][j - v[i]] = max(f[i - 1][j - v[i]],f[i - 1][j - 2 \times v[i]] + w[i],\dots,f[i - 1][j - k \times v[i]] + k \times w[i])$$
将状态 $f[i][j - v[i]]$ 代入 $f[i][j]$ 的状态转移方程中,我们可以得到:
$$f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i])$$
该式与 01 背包 的状态转移方程十分相似,故而可使用相似的空间优化方法 —— 从后往前更新一维数组以更新相关状态。对于完全背包而言,其状态转移方程涉及 $f[i][j - v[i]]$,而非 $f[i - 1][j - v[i]]$,故而其应当从前往后更新一维数组。
状态初始化
与 01 背包 状态初始化相同,我们这样初始化:指定 $f[0][j] = 0,(0 \leq j \leq V)$。
多重背包
题目描述及示例
有 $N$ 件物品和一个容量是 $V$ 的背包。第 $i$ 种物品最多有 $s_i$ 件,每件体积是 $v_i$,价值是 $w_i$。求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大?
1 | Input: |
解题思路
数据存储
v[i]用于存储各物品体积,w[i]用于存储各物品价值,s[i]用于存储各物品个数。状态表示
与 01 背包 状态表示相同,我们可以这样表示状态 $f[i][j]$:从前 $i$ 个物品中选择,并将它们转入容量为 $j$ 的背包中,所能得到的最大价值。
状态转移
该题与 01 背包 和 完全背包 类似,仅是物品可有限次选用,类比于 完全背包 的状态转移方程,其状态转移方程可表示如下:
$$f[i][j] = max(f[i - 1][j],f[i - 1][j - v[i]] + w[i],\dots,f[i - 1][j - k \times v[i]] + k \times w[i]),(j \geq k*w[i] \ 且 \ s[i] \geq k)$$
该状态转移方程所具特性与 01 背包 的状态转移方程所具特性基本一致,故而其可使用相同的空间优化方法 —— 从后往前更新一维数组以更新相关状态。由于其中涉及众多状态取最大值,故而需要使用一个循环完成。
状态初始化
与 01 背包 状态初始化相同,我们这样初始化:指定 $f[0][j] = 0,(0 \leq j \leq V)$。
上面这种属于最基本的解题思路,我们可以发现其时间复杂度为 $O(N \times S \times V)$ ($S$ 表示物品的平均个数)。
接下来我们从另一角度看待多重背包:如果一个物品存在 $m$ 件,我们便将其分解为 $m$ 个数量均为 $1$的不同物品,此时每个物品仅有选与不选两种选择,故而多重背包就转换为 01 背包。
现在我们思考一个问题:将 $m$ 拆分为 $m$ 个 $1$,可以表达 “选择区间 $[0,m]$ 内任意数”,那么有没有更简便地方法以达到此目的?
这种更为简便地方式就是:二进制。例如:我们希望选择区间 $[0,15]$ 内任意数,我们只需要 $(2^0 = 1,2^1 = 2, 2^2 = 4,2^3 = 8)$ 四个数即可;如果我们希望选择区间 $[0,12]$ 内任意数,我们只需要 $(2^0 = 1,2^1 = 2, 2^2 = 4,12-4-2-1=5)$ 四个数即可。
基于二进制,我们重新看待多重背包:如果一个物品存在 $m$ 件,我们便基于二进制将其分解为 $\lceil log_2^m \rceil$ 个具有不同数量的物品,此时每个物品同样仅具有选与不选两种选择,故而多重背包就转换为 01 背包。可以发现:该种解法的时间复杂度降低为 $O(N \times \lceil log_2^{S} \rceil \times V)$ 。
对于多重背包而言,另有一种基于单调队列的优化方案,它可将时间复杂度降低为 $O(N \times V)$。这种方法比较复杂,我们在此简单介绍。
经空间优化后,多重背包的状态表示为 $f[j]$,并且每次循环中,根据当前物品 $i$ 更新状态 $f[j]$ 。根据状态更新流程,我们可将状态分为如下几类:
$$f[0 + k \times v[i]],f[1 + k \times v[i]],\dots,f[m + k \times v[i]](m = v[i] - 1,k \times v[i] \leq V)$$
对于任意一类状态 $f[t + k \times v[i]](0 \leq t < v[i],k \times v[i] \leq V)$,我们构建 $(f[t + k \times v[i]] - k \times w[i],k)$ 键值对 (该式可理解为所有状态在同等基准下的增益),并排序它们。对于任意 $f[j]$ 而言,如果容量、物品数量条件满足,则从具有最大增益的状态转移将会使得更新后的 $f[j]$ 最大,此时具有最大增益的状态就是 $f[j]$ 转移所需的最佳状态。借助于排序,可使得一步找到状态转移所需的最佳状态,如此便可降低时间复杂度。
具体实现中,我们并不需要使用排序,只需使用单调队列即可。
混合背包
题目描述及示例
有 $N$ 种物品和一个容量是 $V$ 的背包,物品一共有三类:
- 第一类物品只能用 $1$ 次 (01背包);
- 第二类物品可以用无限次 (完全背包);
- 第三类物品最多只能用 $s_i$ 次 (多重背包);
每种体积是 $v_i$,价值是 $w_i$。求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大?
1 | Input: |
解题思路
这道题目属于上面三道题目的综合。首先我们可以基于二进制将多重背包转换为 01 背包;对于 01 背包和多重背包而言,二者区别仅在于从后往前更新一维数组还是从前往后更新一维数组,此时根据物品只能使用 $1$ 次还是无限次,动态选择循环方向即可。
二维费用的背包
题目描述及示例
有 $N$ 种物品和一个容量是 $V$ 的背包,背包能承受的最大重量是 $M$。每件物品只能用一次,体积是 $v_i$,重量是 $m_i$,价值是 $w_i$。求解将哪些物品装入背包,可使物品总体积不超过背包容量,总重量不超过背包可承受的最大重量,且价值总和最大?
1 | Input: |
解题思路
数据存储
v[i]用于存储各物品体积,m[i]用于存储各物品重量,w[i]用于存储各物品价值。状态表示
这道题目纯属 01 背包 的二维扩展,故而我们可以这样表示状态 $f[i][j][k]$:从前 $i$ 个物品中选择,并将它们装入容量为 $j$ 、所能承受的最大重量为 $k$ 的背包中,所能得到的最大价值。
状态转移
已有 01 背包 相关知识,该题目的状态转移方程可表示如下:
$$f[i][j][k] = max(f[i - 1][j][k], f[i - 1][j - v[i]][k - m[i]] + w[i]),(j \geq v[i] \ 且 \ k \geq m[i])$$
类比于 01 背包 ,我们可使用二维数组 $f[j][k]$ 优化空间。
状态初始化
根据状态表示,我们可这样初始化:指定 $f[0][j][k] = 0,(0 \leq j \leq V \ 且 \ 0 \leq k \leq M)$。
分组背包
题目描述及示例
有 $N$ 组物品和一个容量是 $V$ 的背包,每组物品有若干个,同一组内的物品最多只能选一个。每件物品的体积是 $v_{ij}$,价值是 $w_{ij}$,其中 $i$ 是组号,$j$ 是组内编号。求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大?
1 | Input: |
解题思路
数据存储
id[i]用于存储各物品组号、v[i]用于存储各物品体积,w[i]用于存储各物品价值。状态表示
与 01 背包 状态表示类似,我们可以这样表示状态 $f[i][j]$:从前 $i$ 个物品组中选择,并将它们转入容量为 $j$ 的背包中,所能得到的最大价值。
状态转移
对于状态 $f[i][j]$ 而言,如果它不选择当前物品组 $i$,则其应当由状态 $f[i - 1][j]$ 转移得到;否则就会选择当前物品组,由于一个物品组中只能选择一个物品,故而其应当由状态 $f[i - 1][j - v[k]],(id[k] = i)$ 转移得到。
$$f[i][j] = max(f[i - 1][j], f[i - 1][j - v[k]] + w[k]),(0 \leq k < id.length \ 且 \ id[k] = i)$$
与 01 背包 类似,其可使用相同的空间优化方法 —— 从后往前更新一维数组以更新相关状态。
状态初始化
与 01 背包 状态初始化类似,我们这样初始化:指定 $f[0][j] = 0,(0 \leq j \leq V)$。
有依赖的背包
题目描述及示例
有 $N$ 个物品和一个容量是 $V$ 的背包,物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。如下图所示:
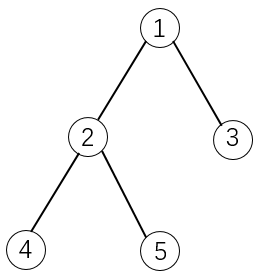
如果选择物品 5,则必须选择物品 1 和 2。这是因为 2 是 5 的父节点,1 是 2 的父节点。
每件物品的编号是 $i$,体积是 $v_i$,价值是 $w_i$,依赖的父节点编号是 $p_i$。物品的下标范围是 $1…N$。求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大?
1 | Input: |
解题思路
数据存储
v[i]用于存储各物品体积,w[i]用于存储各物品价值,graph[i][j]用于存储节点间依赖关系,表示物品 $j$ 依赖于物品 $i$。状态表示
这道题目属于背包 DP 与树形 DP 的结合,比较困难。我们直接定义状态 $f[u][j]$:从物品 $u$ 所在子树中选择物品,并将它们转入容量为 $j$ 的背包中,所能得到的最大价值。
状态转移
对于状态 $f[u][j]$ 而言,如果不选择当前物品,则各子物品都无法选择,可直接置 $f[u][j] = 0$;否则就需要根据子物品及容量动态转移得到。
如果选择当前物品,则其状态转移方程为:
$$f[u][j] = max(f[son][t] + f[u][j - t - v[i]] + w[i]),(son = graph[u][k],0 \leq k < graph[u].length, 0 \leq t \leq j - v[i])$$
如果不选择当前物品,则其状态转移方程为:
$$f[u][j] = 0,(0 \leq j \leq V)$$
如果我们将当前物品的子物品所在子树看做一个个物品组,将具有不同容量的 $f[son][k]$ 看做一个个物品,那么一个物品组中只能选择一个物品,故而这是一个分组背包问题。按照分组背包解法可以求解得到 $f[u][j],(0 \leq j \leq V)$。
状态初始化
此题的状态初始化比较简单,默认不选择所有物品,故而直接指定 $f[u][j] = 0,(0 \leq j \leq V)$。