数据结构-R树

发表于 分类于
本文字数： 2.7k 阅读时长 ≈ 2 分钟

概述

R 树 是一种处理高维空间存储问题的数据结构。值得注意的是：(R 树，B 树) 和 (k-d 树，二叉查找树) 具有类似关系，即前者是后者在高维空间的扩展，不同点在于 R 树是平衡的而 k-d 树是不平衡的。

虽然网上资料显示 “R 树是 B 树在高维空间的扩展”，但是随着对 R 树的深入了解，我觉得 “R 树应当是 B+ 树在高维空间的扩展”。故而我将以 B+ 树为例引出 R 树。

首先看一个 B+ 树示例：

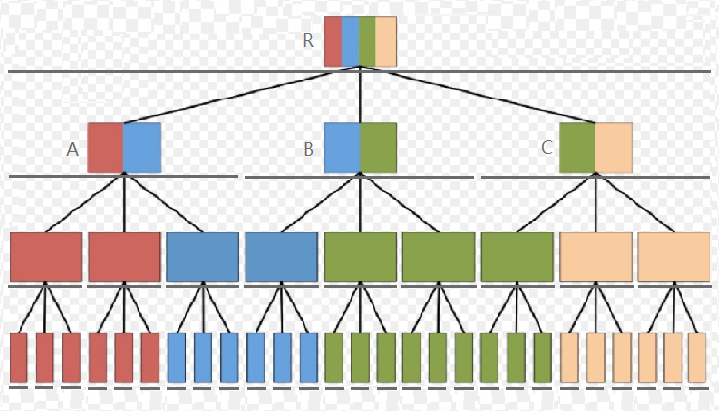
图一：B+树示例

在 B+ 树中，叶节点存放所有关键字及相应数据；索引节点存放索引关键字，根据这些索引关键字可进一步找到部分关键字及其数据，如此我们可称索引节点掌管若干关键字及其数据。例如：R 节点掌管所有关键字及其数据，其下三个子节点 A、B、C 各掌管 R 节点所掌管关键字及其数据的一部分。当进行查询时，首先在 R 节点处根据索引关键字确定待查找关键字在哪个子节点的掌管范围之内，随后递归到子节点中进行处理，直至到达叶节点。如果叶节点中包含指定关键字，则查询成功，否则查询失败。如此一个查询过程，其本质就是基于索引信息逐步缩减待查找范围。

其次我们看一个高维空间查找示例：如何快速查询中国地图内的某一村庄？最愚蠢的办法就是遍历所有村庄，一一比对。而更为高效地做法便是：首先根据村庄位置信息锁定搜索范围到省、市、县、镇，最后在镇中遍历所有村庄，一一比对。

从上述两个例子中可以看出：无论高维空间查询还是低维空间查询，其本质都是建立数据索引，随后在查找过程中逐步缩减待查找范围 (所有加快查询速度的数据结构都是这样做的，只不过缩减时所依据的信息不同而已)。

接下来，简单看看 R 树是如何缩减待查找范围的，这里以二维空间例子说明 (图中仅 R3 区域数据详细标识，其余区域数据直接省略)：

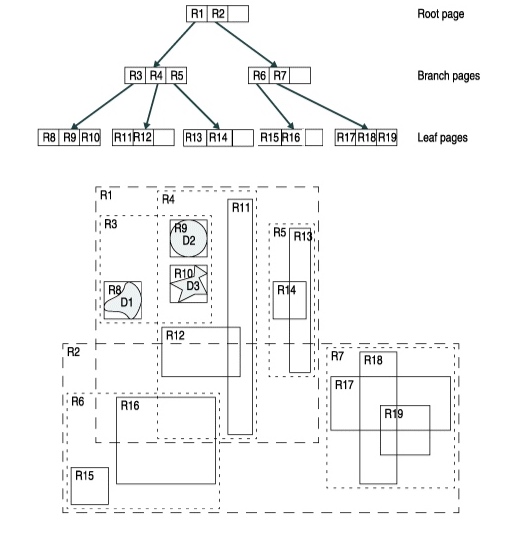
图二：R树示例

关于此图，我们可以这样看：所有点散布于平面之上，根据某些规则首先将点划分为块 R8、R9 … R19；在此基础之上，我们划分块为 R3、R4 … R7；更进一步划分块为 R1、R2；最终划分为一个整块。对于点而言，其中保存关键字 (标识为 ${x,y}$) 及其数据信息；对于块而言，其中保存子块索引及当前块所含点的 MBR 位置信息。当进行查询时，根据待查询关键字及块信息，可逐步缩减查询范围至块 R8、R9 … R19 中之一，然后将其中点信息与待查询关键字一一比对，从而判断查询是否成功。

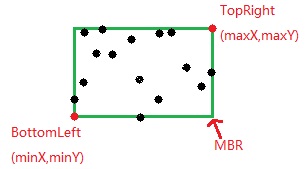
MBR (Minimum Bounding Retangle)：假定存在若干点，最小限定矩形就是可以包含这些点的最小矩形，它可通过获取所有点的最大最小坐标值得到，假定获取的坐标值依次为 $minX,minY,maxX,maxY$，此时最小限定矩形可表示为 ${(minX,minY),(maxX,maxY)}$。

图三：MBR示意图

维基百科中并未给出 R 树具体定义。根据所查资料，基本上可以这样说：R 树定义与 B+ 树定义基本一样，二者不同点则在于节点实现。

下面实现中，我们直接以二维空间中的 R 树为例，以说明各项操作 (不作实现)。当然，二维空间扩展为多维空间是很简单的。

结构

在 B+ 树中，节点分为索引节点和叶节点。R 树中亦是如此，故而这里以伪代码形式给出两种节点结构的详细信息 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Node {
    
}

// 索引节点
class indexNode extends Node {
    // 两者综合表征MBR。
    private Point bottomLeft, TopRight;
    // 子节点索引。
    ArrayList<Node> childrens;
}

// 叶节点
class leafNode extends Node {
    // 两者综合表征MBR。
    private Point bottomLeft, TopRight;
    // 两者共同构建键值对。
    ArrayList<Ponit> keys;
    ArrayList<value> values;
}

实现

查询

查询操作与 B+ 树类似，这里简单描述：

  1. 置当前子树根节点为 $root$。
  2. 如果 $root$ 为索引节点，则一一判断子节点的 MBR 是否与待搜索关键字重合，如果重合则递归处理子节点，并返回递归结果。
  3. 如果 $root$ 为叶节点，则一一判断各关键字是否与待搜索关键字相同，如果相同则返回该关键字及相应数据。

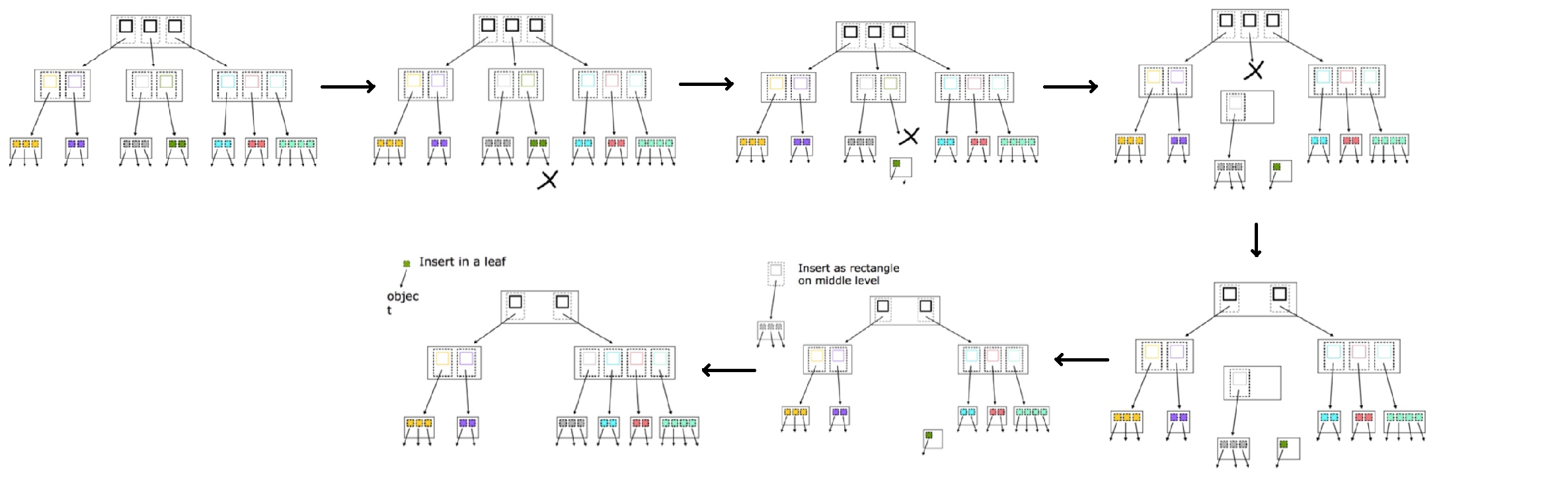
插入

插入操作比较复杂，首先简单描述其过程：

  1. 将待插入关键字及其数据插入至合适的叶节点之中。
  2. 如果叶节点所含关键字个数 (或者索引节点所含关键字个数) 大于阈值，则分裂为两个叶节点。父节点中删除原始节点索引，并新建这两个叶节点的节点索引。
  3. 如果当前节点发生分裂，则递归处理父节点。

关于插入操作，我们需要着重说明两个问题：1. 如何插入至合适叶节点？2. 如何分裂节点？

  1. 如何插入至合适叶节点？

    关于这个问题，R 树具体操作方法是十分巧妙的。简要描述如下：

    • 如果当前节点为叶节点，则直接插入即可。
    • 如果当前节点为索引节点，则首先更新当前节点的 MBR，随后依次遍历所有子节点，找到添加待插入关键字后使得子节点的 MBR 扩张最小的节点 (如果存在多个，则选择 MBR 面积最小的那个节点)，然后递归处理子节点。

    图三：扩张示意图

  2. 如何分裂节点？

    通过执行分裂算法以分裂节点，现有多种分裂算法，最常用地便是二次方方案。

    在二次方方案中，首先，它将两重循环遍历所有子节点，对于任意两个子节点 $N1$ 和 $N2$，计算可包裹这两个节点中所有关键字的 MBR，随后计算增量 $d = MBR - N1.MBR - N2.MBR$，接下来找到具有最大增量的两个子节点 (记为 $d1$ 和 $d2$)，并将它们分别放置到分裂后的两个节点之中。最后，对于其余节点而言，如果该节点距离 $d1$ 更近，则将其放置到 $d1$ 所在的分裂节点之中，否则放置到 $d2$ 所在的分裂节点之中。

    图四：分裂示意图

    增量越大，表明两个节点的对角线距离越远。选择具有最大增量的两个节点，就是选择对角线距离最大的两个节点，如此操作可尽可能保证分裂后两个节点的 MBR 相交较少。

删除

在 B+ 树中，删除指定关键字后，通过借调关键字或合并节点完成调整操作；而在 R 树中，删除指定关键字后，它通过重新插入至 R 树中完成调整操作。具体操作如下：

  1. 找到待删除关键字所在的叶节点，并将该关键字及其数据从中删除。
  2. 如果删除后的叶节点所含关键字 (或者索引节点所含关键字个数) 小于阈值，则将这些关键字及其数据 (或者索引节点) 放置到链表 Q 中，并在父节点中删除对应的节点索引。
  3. 递归处理父节点。
  4. 经过以上调整之后，将 Q 中所有数据重新插入至 R 树之中。如果数据为关键字及其数据，则按照普通插入操作插入即可；如果数据为索引节点，需要将其插入至原先所在层级，如此做的原因在于保证所有叶节点仍然处于同一层级。

图五：删除图例

相关文章