算法-字符串匹配(三)

概述

Sunday 算法是一种经典地字符串匹配算法。它通过简化 BM 算法操作而成，并且实践证明：Sunday 算法查询性能好于 BM 算法，故而该种算法在字符串匹配问题上应用最为广泛。

我们首先简单回顾一下 BM 算法：它采用从后往前方式比较字符，使用坏字符规则和好后缀规则实现跳跃无效匹配。值得注意的是：BM 算法实践之中，有人统计发现：绝大多数地跳跃操作均来自于坏字符规则。另外，由于好后缀表构造比较麻烦而坏字符表构造简单，所以就提出了一种 BM 算法阉割版——仅使用坏字符规则实现跳跃。

Sunday 算法就属于 BM算法阉割版地一种，但是它对坏字符规则进行了修改：在 BM 算法中，匹配失败的字符称为坏字符；而在 Sunday 算法中，匹配失败时参与匹配的最末位字符的下一位字符称为坏字符。举例而言：对于 BM 算法而言，图中 text[1] = 'u' 属于坏字符；对于 Sunday 算法而言，图中 text[6] = 'i' 属于坏字符。

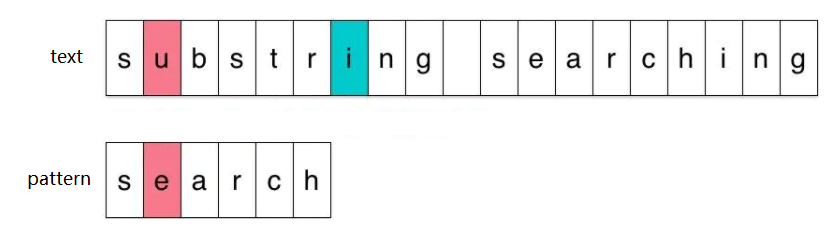
正是由于这样地修改，使得 Sunday 算法并不局限于从后往前比较字符，它同样可以采用从前往后比较字符。

实现

BM 已然实现，这种实现就比较简单。其实现代码如下：

private int[] genBc(String pattern) {
    // 假定所有字符均为ascii，如果存在其他字符，这里也可使用map加以实现。
    int[] bc = new int[256];
    // 初始化为-1，表示未曾出现。
    Arrays.fill(bc, -1);
    
    // 从前往后，根据字符信息覆盖数组该位置原始信息。
    // 正是如此操作，才可保证所存位置信息均为对应字符的最右侧位置。
    for (int i = 0; i < pattern.length(); i++) {
        bc[pattern.charAt(i)] = i;
    }
    
    return bc;
}


public int match(String text, String pattern) {
    // 初始化
    int[] bc = genBc(pattern);

    for (int i = 0; i <= text.length() - pattern.length(); ) {
        int j;
        // 尝试匹配pattern与text[i,i+pattern.length()]
        for (j = pattern.length() - 1; j >= 0 && text.charAt(i + j) == pattern.charAt(j); j--);

         // j=-1表明完全匹配成功，退出即可。
        if (j == -1) {
            return i;
        }

        // 匹配失败，如果坏字符不存在，则直接返回-1。
        if (i + pattern.length() >= text.length()) {
            return -1;
        } else {
            // 获取坏字符，并根据坏字符规则确定移动步数。
            i += (pattern.length() - bc[text.charAt(i + pattern.length())]);
        }
    }

    return -1;
}

时空复杂度

理论证明：最坏时间复杂度为 $O(text.length * pattern.length)$，平均时间复杂度为 $O(text.length)$，空间复杂度为 $O(pattern.length)$。