算法-字符串匹配(一)

发表于 分类于 ，
本文字数： 2.6k 阅读时长 ≈ 2 分钟

概述

字符串匹配：判断模式串 pattern 是否出现于文本串 text 之中。常见匹配算法有：BF、KMP、BM、Sunday。

字符串匹配算法构建十分精妙，往往难于理解，因此我们将通过三篇文章详细介绍字符串匹配算法。第一篇文章介绍 BF 和 KMP 算法，第二篇文章介绍 BM 算法，第三篇文章介绍 Sunday 算法。

BF 算法

BF 全称为 Brute Force，即暴力匹配字符串——遍历 text 所有子串，将其与 pattern 进行匹配，其实现如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int match(String text, String pattern) {
    for (int i = 0; i < text.length() - pattern.length(); i++)  {
        boolean flag = true;
        for (int j = 0; j < pattern.length(); j++) {
            if (text.charAt(i + j) != pattern.charAt(j)) {
                flag = false;
                break;
            }
        }
        if (flag) {
            return i;
        }
    }
    return -1;
}

分析上述代码，容易得知：BF 算法的时间复杂度为 $O(text.length * pattern.length)$，空间复杂度为 $O(1)$。

KMP 算法

BF 算法匹配过程十分粗暴，致使匹配效率过低。那么不由得思考：是否能够借助某些技巧加快匹配过程？换言之，是否能够借助某些事实以尽可能多地跳过无效匹配？

我们首先看一个字符串匹配示例：

图一：字符串匹配示例

此时 text[10] != pattern[6]，故而需要重新匹配。如果按照 BF 算法的尿性，它会置 $i = 5, j = 0$ 并重新匹配 pattern。

我们简单观察字符串 pattern ，可以发现未匹配字符 D 之前的子串 ABCDAB 具有一个性质：前缀 AB 与后缀 AB 相同。另外，观察 text，可以发现 text[10] 之前的子串就是 ABCDAB (原因十分简单：这部分属于匹配成功部分)。

综合这二者观察，我们可以这样执行重新匹配操作：$i$ 标识下标保持不变，置 $j = 2$ (之所以能够置为 2，原因在于：text 未匹配字符之前的内容是 AB (对应 pattern 后缀)，pattern 开始的内容也是 AB (对应 pattern 前缀)，二者相同故无需再次匹配)。 这基本就是 KMP 的思想 —— 借助于相同的前后缀以跳过无效匹配。

在 KMP 中，跳转操作是基于 next[] 实现的，其中 next[j] 具有如下含义：如果 pattern[j] 与 text[i] 匹配失败，则 j 需赋值为 next[j]，随后与 text[i] 再次匹配。如果 next[j] = -1，此时需要置 i = i + 1, j = 0，并重新开始匹配。

匹配过程

我们将基于例子说明 KMP 匹配过程，随后给出 KMP 匹配代码 (这里先不指明 next 如何求取)。

初始状态：

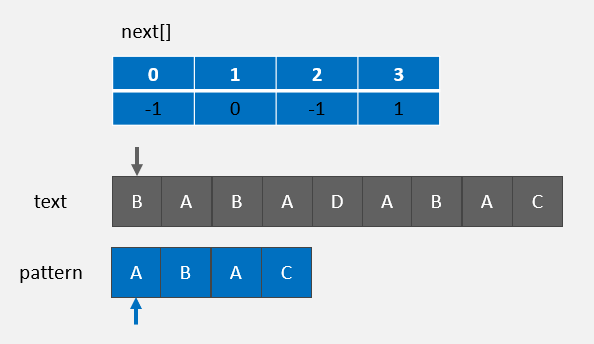
text[0] != pattern[0]，则 j = next[j] = -1，因为 next[j] = -1，故而需要执行 i = i + 1, j = 0 ：

text[1,2,3] = pattern[0,1,2]，则继续比较下一位：

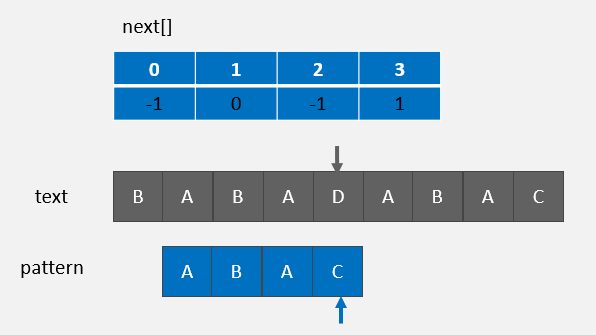
text[4] != pattern[3]，则 j = next[j] = 1 ：

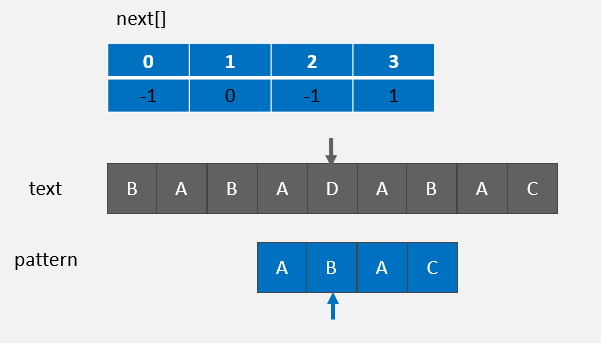
text[4] != pattern[1] ，则 j = next[j] = 0 ：

text[4] != pattern[0]，则 j = next[j] = -1，因为 next[j] = -1，故而需要执行 i = i + 1, j = 0 ：

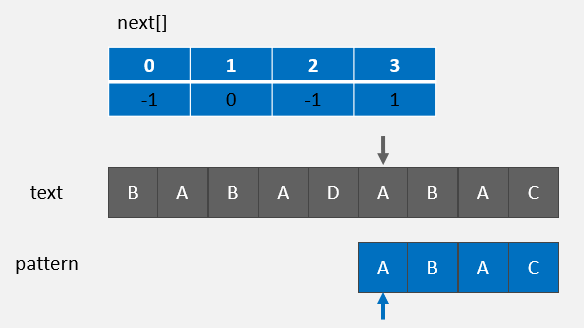
text[5,6,7,8] = pattern[0,1,2,3] ，匹配成功。

根据上述过程，可以知道：在 KMP 匹配过程中，i 总是向前行进地，j 则随 next[] 进行调整。

KMP 匹配实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public int match(String text, String pattern) {
    // 获取next[]。
    int[] next = getNext(pattern);
    
    for (int i = 0, j = 0; i < text.length(); ) {
        // j=-1或者字符匹配成功，i,j均加一。
        if (j == -1 || text.charAt(i) == pattern.charAt(j)) {
            i++;
            j++;
        } else {
            // 字符匹配失败，j根据next[]进行调整。
            j = next[j];
        }

        // 表明pattern中所有字符均已匹配，则返回匹配字符子串的开始位置。
        if (j == pattern.length()) {
            return i - j;
        }
    }
    
    // 匹配失败，返回-1。
    return -1;
}

next 求取

next[] 求取过程比较复杂，我们直接给代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
private int[] getNext(String pattern) {
    int[] next = new int[pattern.length()];
    
    // 初始化。
    next[0] = -1;
    int i = 0, j = -1;
    
    while (i < next.length - 1) {
        if (j == -1 || pattern.charAt(i) == pattern.charAt(j)) {
            i++;
            j++;
            next[i] = j;
            // 这几行注释代码是对 next[i]=j 的进一步优化。
            // next[j]表示匹配失败时需要重新匹配的下标位置。如果i,j所在字符相同，则当i所示字符与text中指定字符匹配失败时，重新匹配下标位置j也一定会匹配失败，故而这里直接赋值next[j]。
            // if (pattern.charAt(i) == pattern.charAt(j)) {
            //     next[i] = next[j];
            // } else {
            //     next[i] = j;
            // }
        } else {
            j = next[j];
        }
    }
    return next;
}

如果 next 求取实现代码看不懂，可以先看一下 优化求解前缀函数。

时空复杂度

理论证明：时间复杂度为 $O(text.length + pattern.length)$，空间复杂度为 $O(pattern.length)$。