数据结构-后缀数组

发表于 2020-08-02 分类于数据结构与算法

本文字数： 6.8k 阅读时长 ≈ 6 分钟

概述

后缀数组 是特定字符串的所有后缀有序排列而成的一个数组。它比后缀树更为实用，常用于全文索引。

其结构图大致如下：

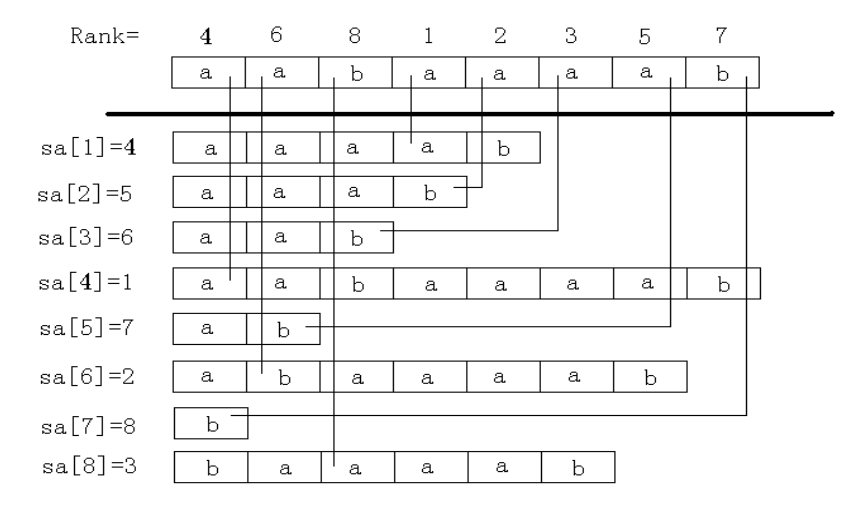
后缀数组比较特殊，本文简单介绍其构建方法及应用。

构建

后缀数组并非直接存储后缀，而是后缀在特定字符串中的起始下标。

我们在此说明如下构造算法中可能使用到的重要变量名称：

sa[i] ：排名为 $i$ 的后缀在特定字符串中的起始下标。
rk[i] ：起始下标为 $i$ 的后缀在所有后缀中的排名。
height[i] ：排名为 $i$ 的后缀与排名为 $i - 1$ 的后缀的最长公共前缀。
LCP(str1,str2) ：两个字符串的最长公共前缀。
sub[i][k] ：特定字符串区间 $[i,i + 2^k - 1]$ 所表示的子串。
sa[i][k] ：长度为 $2^k$ 的所有子串中，排名为 $i$ 的子串在特定字符串中的起始下标。
rk[i][k] ：长度为 $2^k$ 的所有子串中，起始下标为 $i$ 的子串在所有子串中的排名。
prefixs[i] ：特定字符串的前缀哈希值。
squares[i] ：存放 $2^i$ 系列值。

结构

class SuffixArray {
    // 特定字符串
    private String T;
    // 排名对应起始下标数组(下标从1开始)
    private Integer[] sa;
    // 起始下标对应排名数组(下标从1开始)
    private Integer[] rk;
    ...
}

朴素构造算法

朴素构造算法十分简单：排序所有后缀，然后按顺序存储各后缀在特定字符串中的起始下标。

排序操作的时间复杂度为 $O(Nlog^N)$，比较字符串的时间复杂度为 $O(N)$，故而该构造算法的时间复杂度为 $O(N^2log^N)$。

public SuffixArray(String T) {
    // 添加前缀，方便后续代码编写。
    T = "$" + T;
    this.T = T;
    this.sa = new Integer[T.length()];

    // 初始化sa
    for (int i = 1; i < this.sa.length; i++) {
        this.sa[i]= i;
    }

    Arrays.sort(this.sa, 1, this.sa.length, (o1, o2) -> {
        int index1 = (int) o1;
        int index2 = (int) o2;
        return this.T.substring(index1).compareTo(this.T.substring(index2));
    });
}

二分思想 + Hash 优化

针对朴素构造算法中的字符串比较操作，我们可基于二分思想及 Hash 将其时间复杂度优化为 $O(log^N)$。

该优化操作源于如下观察：通过比较最长公共前缀所在位置的下一个字符，即可得到两个字符串的大小关系。

为获取最长公共前缀所在位置，我们可使用二分思想：如果 $[l1, l1 + mid - 1]$ 表示字符串的哈希值与 $[l2,l2 + mid - 1]$ 表示字符串的哈希值相等，表明最长公共前缀所在位置处于右半部分，否则表明最长公共前缀所在位置处于左半部分。

采用的哈希函数为：$\sum_{i = l}^{i = r}2^i * T[i]$ 。

如果需要获取指定区间 $[L,R]$ 表示字符串的哈希值，可借由前缀哈希值数组 prefixs 和 $2^k$ 预存数组 squares 推导得到：$(prefixs[R] - prefixs[L - 1]) / squares[L]$ 。

mid 表示步长 (与普通二分算法中 mid 含义不同)。

由于字符串比较操作的时间复杂度降为 $O(log^N)$，故而该构造算法的时间复杂度为 $O(N(log^N)^2)$ 。

public SuffixArray(String T) {
    // 添加前缀，方便后续代码编写。
    T = "$" + T;
    this.T = T;
    this.sa = new Integer[T.length()];
	this.prefixs = new Integer[this.T.length()];
    this.squares = new Integer[this.T.length()];
    prefixs[0] = '$' - 'a';
    squares[0] = 1;
    
    // 初始化相关数组
    for (int i = 1; i < this.sa.length; i++) {
        this.sa[i]= i;
        squares[i] = squares[i - 1] * 2;
        prefixs[i] = prefixs[i - 1] + (this.T.charAt(i) - 'a') * squares[i];
    }

    Arrays.sort(this.sa, 1, this.sa.length, (o1, o2) -> {
        int index1 = (int) o1;
        int index2 = (int) o2;

        // 定义步长左端、右端。
        int l = 0, r = Math.min(this.T.length() - index1, this.T.length() - index2);
        while (l < r) {
            // 获取中间步长
            int mid = (l + r) >> 1;

            // 获取相应子串的哈希值
            int strHash1 = (prefixs[index1 + mid - 1] - prefixs[index1 - 1]) / squares[index1];
            int strHash2 = (prefixs[index2 + mid - 1] - prefixs[index2 - 1]) / squares[index2];

            // 如果二者不等，表明步长应小于等于mid，否则表明步长应大于mid。
            if (strHash1 != strHash2) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
		
        // 二分过程后，[index1,index + l - 1 - 1]对应字符串为最长公共前缀，那么只需比较对应位置下一个字符即可。
        return this.T.charAt(index1 + l - 1) - this.T.charAt(index2 + l - 1);
    });
}

倍增思想

上述两种算法将两个后缀视为独立字符串进行比较，倍增思想则考虑后缀之间的内在联系。

倍增思想中主要涉及如下三个数组：sub[i][k] 、rk[i][k] 、sa[i][k] 。

假定我们已经获知 $sub[i][k]$ 对应排名为 $rk[i][k]$。如果需要判断任意两个子串 $sub[i][k+1]$ 和 $sub[j][k+1]$ 之间的大小关系，只需先行比较 $sub[i][k]$ 与 $sub[j][k]$ 对应排名，如果二者排名相同，则再比较 $sub[i + 2^k][k]$ 和 $sub[j + 2^k][k]$ 对应排名。

按照上述描述，基于 $rk[i][k]$ 可顺利推导得到长度为 $2^{k+1}$ 的各子串排序 (亦即 $sa[i][k+1]$)，基于 $sa[i][k+1]$ 又可方便得到 $rk[i][k+1]$。如此循环迭代，最终我们将得到 $sa[i][k],2^k \geq T.length$，此亦为特定字符串 $T$ 的后缀数组。

现在问题就在于：如何排序各子串得到 $sa[i][k+1]$ ？

一种可行做法是直接调用快速排序等方式。由于快速排序等方式的时间复杂度为 $O(Nlog^N)$，倍增循环 $O(log^N)$ 次，故而此时构造算法的时间复杂度为 $O(N(log^N)^2)$ 。

一种更为优秀做法是使用基数排序，这是因为 $rk[i][k + 1] \in (0,T.length)$ 。此时排序方式的时间复杂度为 $O(N)$，外加倍增循环 $O(log^N)$ 次，故而此时构造算法的时间复杂度为 $O(Nlog^N)$ 。

我们在此实现第二种做法。

实现代码与描述存在些许出入，故而在此总结一下：

由于需要使用 $rk[i + 2^k][k]$，故而 $rk[i][k]$ 数组空间大小至少为特定字符串长度的两倍。由于 $rk[i][k]$ 数组与特定字符串存在一一对应关系，我们默认 $T[i] = ‘Null’, i \in [T.length,T.length * 2)$ ($Null$ 表示 ascii 码中的空字符)。
最初需要初始化 rk[i][0] 和 sa[i][0]。rk[i][0] 可直接使用对应字符的 ascii 码进行赋值 (如果 $i \geq T.length$，由于 $T[i]$ 为空，故而可设 rk[i][0] = 0)，随后基于基数排序可得到 sa[i][0] 。
由于最初使用 ascii 码赋值 rk[i][0]，故而 rk[] 和 cnt[] (基数排序中的桶) 空间最小需设为最大 ascii 码值。
倍增循环中，我们需要根据 $sub[i][k]$ 和 $sub[i + 2^k][k]$ 对应排名进行排序各子串。当使用基数排序进行排序各子串时，我们首先使用 $sub[i + 2^k][k]$ 对应排名(第二关键字) 排序各子串，然后使用 $sub[i][k]$ 对应排名 (第一关键字) 排序各子串即可。
代码实现中采用数组实现基数排序。

public SuffixArray(String T) {
    // 添加前缀，方便后续代码编写。
    T = "$" + T;
    this.T = T;
    this.sa = new Integer[T.length()];
    this.rk = new Integer[1000];

     // 桶
    Integer[] cnt = new Integer[1000];
    // 临时存放sa
    Integer[] id = new Integer[this.T.length()];
    // 存放旧rank
    Integer[] oldRank;

    // 初始置0
    Arrays.fill(cnt, 0, cnt.length, 0);
    Arrays.fill(this.rk, 0, this.rk.length, 0);

    // 使用基数排序初始化。
    for (int i = 1; i < this.T.length(); i++) {
        this.rk[i] = Integer.valueOf(this.T.charAt(i));
        ++cnt[this.rk[i]];
    }
    for (int i = 1; i < cnt.length; i++) {
        cnt[i] += cnt[i - 1];
    }
    for (int i = this.T.length() - 1; i >=1 ; i--) {
        this.sa[cnt[this.rk[i]]--] = i;
    }

    for (int w = 1; w < this.T.length(); w = w * 2) {
        // 清空桶
        Arrays.fill(cnt, 0, cnt.length, 0);

        for (int i = 1; i < this.T.length(); i++) {
            id[i] = this.sa[i];
        }
        // 基数排序第二关键字
        for (int i = 1; i < this.T.length(); i++) {
            ++cnt[this.rk[id[i] + w]];
        }
        for (int i = 1; i < cnt.length; i++) {
            cnt[i] += cnt[i - 1];
        }
        for (int i = this.T.length() - 1; i >= 1; i--) {
            this.sa[cnt[this.rk[id[i] + w]]--] = id[i];
        }

        // 清空桶
        Arrays.fill(cnt, 0, cnt.length, 0);
        for (int i = 1; i < this.T.length(); i++) {
            id[i] = this.sa[i];
        }
        // 基数排序第一关键字
        for (int i = 1; i < this.T.length(); i++) {
            ++cnt[this.rk[id[i]]];
        }
        for (int i = 1; i < cnt.length; i++) {
            cnt[i] += cnt[i - 1];
        }
        for (int i = this.T.length() - 1; i >= 1; i--) {
            this.sa[cnt[this.rk[id[i]]]--] = id[i];
        }

        oldRank = Arrays.copyOf(this.rk, this.rk.length);

        // 更新rank。
        for (int p = 1, i = 1; i < this.T.length(); i++) {
            if (i == 1 || (oldRank[this.sa[i]] == oldRank[this.sa[i - 1]] && oldRank[this.sa[i] + w] == oldRank[this.sa[i - 1] + w])) {
                this.rk[this.sa[i]] = p;
            } else {
                this.rk[this.sa[i]] = ++p;
            }
        }
    }
}

存在 $O(N)$ 复杂度构建后缀数组的方法，但是由于其过于复杂并不常用，故而不再介绍。

求取 Height

上面的构造算法仅能初始化数组 $sa[i]$ 和 $rk[i]$，数组 $height[i]$ 需单独初始化。

初始化数组 $height[i]$ 仍然存在多种方法，我们一一讲述：

暴力解法

遍历整个数组，每次按序比较两个字符串，从而得到最长公共前缀。

容易得知：此种解法的时间复杂度为 $O(N^2)$。
二分 + hash

对应第二种构造算法。

容易得知：此种解法的时间复杂度为 $O(Nlog^N)$。

线性解法

线性解法基于一个定理：

$height[rk[i]] \geq height[rk[i - 1]] - 1，height[rk[i]] \approx LCP(suffix(i), suffix(rk[i] - 1))$。

该定理证明比较简单，在此简单说明：

当 $height[rk[i - 1]] \leq 1$ 时，$height[rk[i]]$ 需要大于等于零，这显然成立。
当 $height[rk[i - 1]] > 1$ 时，我们可以得知：$suffix(i - 1)$ 与 $suffix(rk[i - 1] - 1)$ 的最长公共前缀大于 $1$。我们将第一个公共字符消去，则此时二者的最长公共前缀变为 $height[rk[i - 1]] - 1$。由于 $suffix(i - 1)$ 消去第一个字符的结果就是 $suffix(i)$，那么可以知道 $height[rk[i]]$ 的结果至少等于 $height[rk[i - 1]] - 1$。

基于这个定理，我们可按照 $height[rk[i]]$ 顺序递推求解高度：

private void calHeight() {
    // k = height[rk[i - 1]]
    for(int i = 1, k = 0; i < this.T.length(); i++) {
        // height[rk[i]] >= height[rk[i - 1]] - 1，故而k值需减一
        if (k > 0) {
            k--;
        }

        // 从k开始继续探索当前后缀与对应排名的上一个后缀相应位置字符是否相等，相等则继续探索，否则k对应就是最长公共前缀。
        while (this.T.charAt(i + k) == this.T.charAt(this.sa[this.rk[i] - 1] + k)) {
            k++;
        }
       
        this.height[this.rk[i]] = k;
    }
}

顾名思义：此种解法的时间复杂度为 $O(N)$。

应用

两后缀最长公共前缀

对于相邻后缀而言，其最长公共前缀就是 $height[i]$。

对于不相邻后缀而言，由于所有后缀按照字典序进行排序，故而不相邻后缀的最长公共前缀应当等于此二者在数组 $sa$ 对应区间内 $height[i]$ 的最小值。

不同子串的数目

子串最初被定义为 $T[i,j]$，当然它也可以被定义为某个后缀的前缀。

那么为求解不同子串数目，我们可以首先计算所有子串的数目，随后减去公共前缀的数目即可。

故而不同子串数目 $sum = (N * (N + 1)) / 2 - \sum height[i]$。