数据结构-权值线段树

发表于 分类于
本文字数： 3.1k 阅读时长 ≈ 3 分钟

概述

权值线段树 属于一种特殊的线段树。普通线段树基于元素个数开辟节点空间，节点之内维护特定信息 (例如，区间最大值、区间最小值)，权值线段树则基于元素值域开辟节点空间，节点之内维护当前区间内的元素个数。

其结构图大致如下：

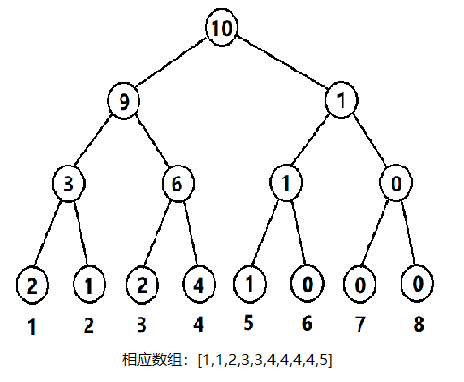
图一：权值线段树

由于节点维护当前区间内的元素个数，故而权值线段树可以 $O(log^N)$ 时间查找整个区间内第 $K$ 大/小元素。

权值线段树具有一个非常重要的性质：假定所有元素按序尾部插入到数组之中，那么数组 $[0,R]$ 对应的权值线段树减去数组 $[0,L-1]$ 对应的权值线段树就是数组 $[L,R]$ 对应的权值线段树。如果保存以往的权值线段树，那么就可以在 $log^N$ 时间复杂度内实现查询任意指定区间 $[L,R]$ 内的第 $K$ 大/小元素，这也是主席树的基本思想。

  • 如果了解桶排序，容易知道：权值线段树维护的是桶信息。

结构

在 数据结构-线段树 中，我们直接使用数组实现线段树。这里采用一种不同的写法，我们选用静态链表进行实现。另外我们直接指定元素类型为 int 。

1
2
3
4
5
6
7
8
9
10
11
12
class WeightSegmentTree {
    // 权值数组
    private int[] tree;
    // 左儿子
    private int[] left;
    // 右儿子
    private int[] right;
    // 节点计数(以此方式指定左右儿子节点在tree中位置)
    private int nodeCount;
    // 最大边界，故而值域范围为[0,1000]
    public static final int Bound = 1000;
}

实现

辅助方法

  • 构建权值线段树

    以 root 为根节点、所负责区间为 $[l,r]$ 的子树基于含有元素个数信息的 sum 进行构建权值线段树。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    private void build(int root, int l, int r, HashMap<Integer, Integer> sum) {
        // 区间内仅有一个值，则赋值sum中该值对应的个数，如果没有就赋值为0。
        if (l == r) {
            this.tree[root] = sum.containsKey(l) ? sum.get(l) : 0;
            return ;
        }

        // 获取中间位置。
        int mid = (l + r ) >> 1;
        
        // 基于nodeCount构建左右儿子节点。
        this.left[root] = ++nodeCount;
        this.right[root] = ++nodeCount;

        // 递归构建左右子树。
        build(this.left[root], l, mid, sum);
        build(this.right[root], mid + 1, r, sum);

        // 更新根节点值。
        this.tree[root] = this.tree[this.left[root]] + this.tree[this.right[root]];
    }

  • 当前子树内查询第 $K$ 小元素 ($K \in[0,\infty)$)

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    private int getKthTree(int root, int l, int r, int k) {
        // 当前子树所负责区域仅有一个值，如果对应元素个数大于k，则返回该元素，否则表明不存在，直接返回一个负数。
        if (l == r) {
            return (this.tree[root] > k) ? l : -WeightSegmentTree.Bound;
        }

        // 获取中间位置。
        int mid = (l + r) >> 1;
        
        // 获取左子树所负责区间中的元素个数
        int x = this.tree[this.left[root]];
        
        // x>k，表明第k小元素在左子树之中，故而应在左子树中进行查询；否则在右子树中进行查询。
        if (x > k) {
            return getKthTree(this.left[root], l, mid, k);
        } else {
            return getKthTree(this.right[root], mid + 1, r, k - x);
        }
    }

    第 $K$ 大元素代码与此类似，故不赘述。

  • 当前子树插入/删除指定元素若干次

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    private void update(int root, int l, int r, int num, int count) {
        if (l == r) {
            // 如果更新有效，则更新，否则不更新。
            this.tree[root] = (this.tree[root] + count >= 0) ? this.tree[root] + count : this.tree[root];
            return ;
        }
        
        // 获取中间位置。
        int mid = (l + r) >> 1;
        
        // 根据中间位置判断指定元素位于何处。如果位于左子树，则在左子树中更新，否则在右子树中更新。
        if (mid >= num) {
            update(this.left[root], l, mid, num ,count);
        } else {
            update(this.right[root], l, mid, num ,count);
        }
        
        // 更新根节点值。
        this.tree[root] = this.tree[this.left[root]] + this.tree[this.right[root]];
    }

    初始化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public WeightSegmentTree(int[] arr) {
    // 为各数组赋予足够大的空间。
    this.tree = new int[WeightSegmentTree.Bound << 5];
    this.left = new int[WeightSegmentTree.Bound << 5];
    this.right = new int[WeightSegmentTree.Bound << 5];
    this.nodeCount = -1;

    // 统计各元素的个数信息。
    HashMap<Integer, Integer> sum = new HashMap<>();
    for (int element : arr) {
        if (sum.containsKey(element)) {
            sum.replace(element, sum.get(element) + 1);
        } else {
            sum.put(element, 1);
        }
    }

    // 构建根节点
    int root = ++this.nodeCount;
    build(root, 0, WeightSegmentTree.Bound, sum);
}

查询

  • 查询第$K$小元素

    1
    2
    3
    public int getKth(int k) {
        return getKthTree(0, 0, WeightSegmentTree.Bound, k);
    }

    操纵

  • 插入/删除指定元素若干次

    1
    2
    3
    4
    5
    6
    7
    8
    public void update(int num, int count) {
        // 如果该值不在当前值域之中，则直接返回。
        if (num < 0 || num > WeightSegmentTree.Bound) {
            return ;
        }
        
        update(0, 0, WeightSegmentTree.Bound, num, count);
    }
相关文章