数据结构-主席树

发表于 分类于
本文字数： 5k 阅读时长 ≈ 5 分钟

概述

主席树 全称为 “可持久化权值线段树”，它可在 $O(log^N)$ 时间复杂度内实现查询任意指定区间 $[L,R]$ 内的第 $K$ 大/小元素。

其结构图大致如下：

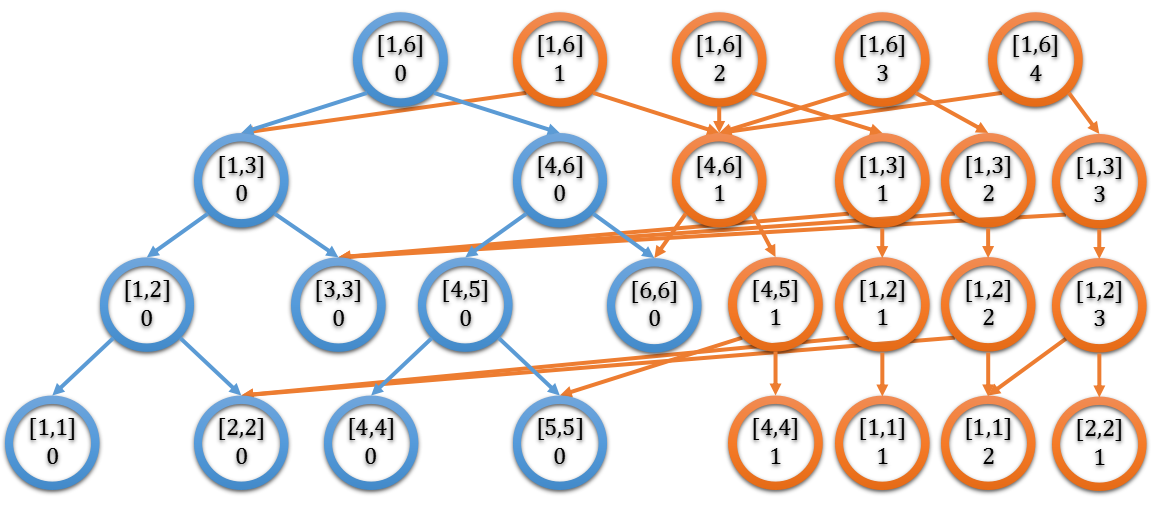
图一：主席树

主席树基于权值线段树实现，故而首先说明权值线段树的两个性质：

  1. 权值线段树可以 $O(log^N)$ 时间查找整个区间内第 K 大/小元素。
  2. 假定所有元素按序尾部插入到数组之中，那么数组 $[0,R]$ 对应的权值线段树减去数组 $[0,L-1]$ 对应的权值线段树就是数组 $[L,R]$ 对应的权值线段树。

基于上述两个性质，可以知道：如果保存插入任意元素后的所有权值线段树，那么就可实现在 $O(log^N)$ 时间复杂度内实现查询任意指定区间 $[L,R]$ 内的第 $K$ 大/小元素。如果保存所有权值线段树，其所需空间将是无法承受的。

观察权值线段树的插入操作，可以发现：一次操作仅会使得对应路径上的 $log^N$ 个节点内容发生变化。故而我们可以通过共用未修改节点使得所需空间降下来。当然，这也就是主席树的基本思想。

结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class HJTTree{
    // 权值数组
    private int[] tree;
    // 历史根节点数组(基于此找到历史权值线段树)
    private int[] root;
    // 左儿子
    private int[] left;
    // 右儿子
    private int[] right;
    // 节点计数
    private int nodeCount;
    // 最新根节点位置
    private int rootIndex;
    // 最大边界
    public static final int Bound = 1000;
}

实现

辅助方法

  • 构建空的权值线段树

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    private void build(int root, int l, int r) {
        // 当前子树所负责区间仅有一个值，故直接赋值0即可。
        if (l == r) {
            this.tree[root] = 0;
            return ;
        }

        // 获取中间位置。
        int mid = (l + r) >> 1;
        
        // 基于nodeCount构建左右儿子节点。
        this.left[root] = ++this.nodeCount;
        this.right[root] = ++this.nodeCount;

        // 递归构建左右子树。
        build(this.left[root], l, mid);
        build(this.right[root], mid + 1, r);
        
        // 子树构建结果为空子树，故而无需更新根节点值。
    }

  • 当前子树插入指定元素

    插入指定元素过程中所经过路径上的节点均需拷贝以生成新节点，并更新这些节点的内容。这样新节点与未曾更改的旧节点就构成了插入指定元素后所对应的权值线段树。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    private int updateTree(int root, int l, int r, int k) {
        // 复制该节点，并更新节点信息。
        int newNode = ++this.nodeCount;
        this.left[newNode] = this.left[root];
        this.right[newNode] = this.right[root];
        this.tree[newNode] = this.tree[root] + 1;

        // 当前子树所负责区间仅有一个值，则直接返回复制的节点即可。
        if (l == r) {
            return newNode;
        }

        // 获取中间位置。
        int mid = (l + r) >> 1;
        
        // 如果mid>=k，表明k应当位于左子树之中，故而需在左子树中进行更新；否则需在右子树中进行更新。
        if (mid >= k) {
            this.left[newNode] = updateTree(this.left[newNode], l, mid, k);
        } else {
            this.right[newNode] = updateTree(this.right[newNode], mid + 1, r, k);
        }

        // 插入元素的结果便是所经路径上各节点的值加一，第六行代码已经加过了，故而无需再更新根节点值。
        return newNode;
    }

  • 查询指定区间内第 $k$ 小元素

    ”概述“ 中通过二者相减得到指定区间 $[L.R]$ 对应的权值线段树，然后在此树上进行查找第 $k$ 小元素。实际代码实现中，这两步可直接合为一步，具体如代码示。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    private int getKthTree(int startRoot, int endRoot, int l, int r, int k) {
        // 当前子树所负责区域仅有一个值，如果对应元素个数(指代[L,R]对应权值线段树中的元素个数)大于k，则返回该元素，否则表明不存在，直接返回一个负数。
        if (l == r) {
            return (this.tree[endRoot] - this.tree[startRoot] > k) ? l : -HJTTree.Bound;
        }

        // 获取中间位置。
        int mid = (l + r) >> 1;
        // 获取[L,R]对应权值线段树中左子树所包含的元素个数
        int x = this.tree[this.left[endRoot]] - this.tree[this.left[startRoot]];

        // 如果x>k，表明第k小元素位于左子树之中，故而应在左子树中进行查找；否则应在右子树中进行查找。
        if (x > k) {
            return getKthTree(this.left[startRoot], this.left[endRoot], l, mid, k);
        } else {
            return getKthTree(this.right[startRoot], this.right[endRoot], mid + 1, r, k - x);
        }
    }

    初始化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public HJTTree(int[] arr) {
    // 为各数组赋予足够大的空间。
    this.tree = new int[HJTTree.Bound << 5];
    this.root = new int[HJTTree.Bound << 5];
    this.left = new int[HJTTree.Bound << 5];
    this.right = new int[HJTTree.Bound << 5];

    // 初始化各字段
    this.nodeCount = -1;
    this.rootIndex = -1;

    // 在this.root[0]处构建空的权值线段树
    this.root[++this.rootIndex] = ++this.nodeCount;
    build(this.root[this.rootIndex], 0, HJTTree.Bound);

    // 将元素依次插入，从而构建权值线段树集。
    for (int i = 0; i < arr.length; i++) {
        update(arr[i]);
    }
}

查询

  • 查询指定区间内的第$K$ 小元素

    代码实现与 “概述” 中的描述同样有些不同。由于初始化时 this.root[0] 对应空权值线段树，故而区间 $[0,R]$ 对应的权值线段树为 this.root[r + 1]、区间 $[0,L]$ 对应的权值线段树为 this.root[l + 1]。此时按照 “概述” 所述，区间 $[L,R]$ 对应的权值线段树为 this.root[r + 1] - this.root[l]。

    1
    2
    3
    public int getKth(int l, int r, int k) {
        return getKthTree(this.root[l], this.root[r + 1], 0, HJTTree.Bound, k);
    }

    操纵

  • 插入指定元素

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    public void update(int k) {
        // 如果该值不在当前值域之中，则直接返回。
        if (k < 0 || k > HJTTree.Bound) {
            return ;
        }
        
        // 每次插入元素后，需更新this.root[]。
        ++this.rootIndex;
        this.root[this.rootIndex] = updateTree(this.root[this.rootIndex - 1], 0, HJTTree.Bound, k);
    }

    扩展

另有两种数据结构可在 $O(log^N)$ 时间复杂度内实现查询任意指定区间 $[L,R]$ 内的第 $K$ 大/小元素——划分树和归并树。前者基于线段树和快速排序而成，后者基于线段树和归并排序而成。在这两种数据结构中，线段树中节点维护的不再是特定信息 (例如区间最大值)，而是区间具体内容。

划分树

  • 构建过程

    假定初始数组为 a，排序后的数组为 b。首先置 level0 为初始数组，故而其所负责区间为 $[0,a.length -1]$；随后利用 level0 所负责区间所在数组的中间值 (即 $b[a.length / 2]$) 将当前区间及所在数组划分为左右两部分，这两部分将构成 level1，随后递归处理 level1 左右两部分以构成最终的线段树。

    另外在构建过程中，每个层级区间所在数组中每个元素 $i$ 还会存储 cnt 信息，它表示当前区间前 $i - 1$ 个元素被划分到左半部分的元素个数。

    划分过程中两点需要注意：

    1. 如果中间值存在多个，需保证一部分中间值位于左半部分，一部分中间值位于右半部分。为达到这一目的，我们需要统计小于中间值的元素个数，按照左半部分区间大小即可确定左半部分需要放置的中间值个数。
    2. 划分过程需保证 元素相对顺序保持不变。例如：level1 中 [3, 1, 4, 2] 一定可以在 [5, 3, 1, 7, 4, 2, 8, 6] 上按序找到，而不会发生元素顺序倒逆的情况。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    a: [5, 3, 1, 7, 4, 2, 8, 6]
    b: [1, 2, 3, 4, 5, 6, 7, 8]

    level0: [5, 3, 1, 7, 4, 2, 8, 6] 
        cnt:[0, 0, 1, 2, 2, 3, 4, 4]
    level1: [3, 1, 4, 2][5, 7, 8, 6] 
        cnt:[0, 0, 1, 1][0, 1, 1, 1]
    level2: [1, 2][3, 4][5, 6][7, 8] 
        cnt:[0, 1][0, 1][0, 1][0, 1]
    level3: [1][2][3][4][5][6][7][8] 
        cnt:[0][0][0][0][0][0][0][0] (这行信息没意义)

  • 查询过程

    假定当前节点所在区间为 $[l,r]$、查找指定区间 $[L,R]$ 内的第 $K$ 个元素，$count = cnt[R + 1] - cnt[L]$ 即表示当前区间有多少个元素进入了左子树。如果 $count > K$，则表明我们需在左子树中查找第 $K$ 个元素，由于元素区间已经发生变化，所以我们需要更新区间为 $[l + cnt[L],l + cnt[R + 1] - 1]$ ；否则我们需要在右子树中查找第 $K - count$ 个元素，此时更新区间为 $[mid + 1 + L - l - cnt[L],mid + 1 + R - l - cnt[R]]$。

    可以如此更新区间的原因在于：划分过程中元素相对顺序保持不变。

归并树

  • 构建过程

    由于归并排序过程与线段树构建过程高度一致，因此可以很容易构建归并树：

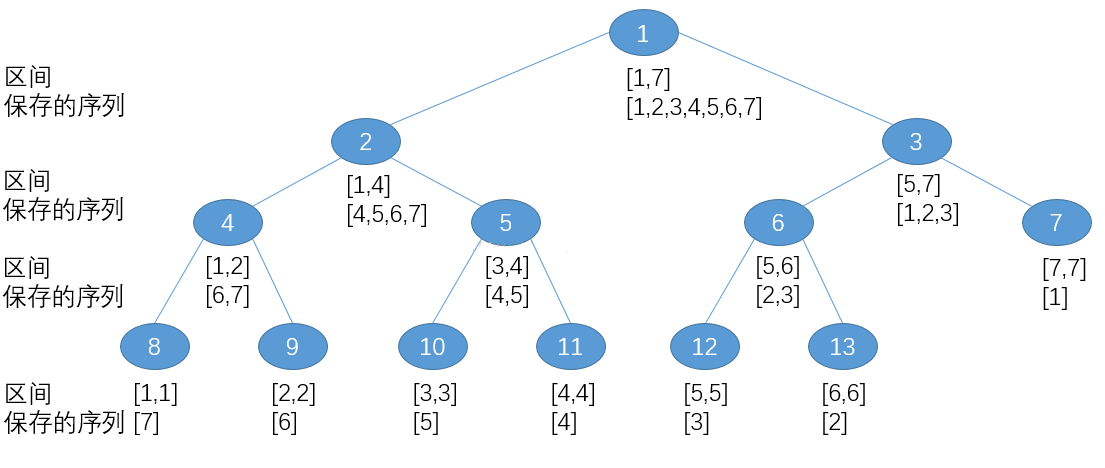
    图二：构建归并树

  • 查询过程

    归并树的查询过程比较废物。

    为完成查询过程，首先需要构建一个函数 rank，它用于查询指定元素 x 在待查找区间 $[L,R]$ 中属于第几小元素。我们可以从线段树根节点开始，如果当前子树根节点所在区间在 $[L,R]$ 之内，则使用二分查找判断 x 在当前区间内属于第几小元素，否则递归左右子树，并将左右子树递归结构相加返回。二分过程的时间复杂度为 $O(log^N)$，查找区间过程的时间复杂度平均为 $O(log^N)$，故而该函数的时间复杂度平均为 $O(log^N * log^N)$ 。

    由于线段树根节点所保存数组为有序的，那么我们可以再次使用二分算法搜索待查找区间 $[L,R]$ 内的第 $K$ 小元素。我们首先取中间位置元素，并且假定该元素为待查找区间 $[L,R]$ 中第 $k$ 小元素。如果 $k > K$，则待查找区间 $[L,R]$ 内的第 $K$ 小元素应当位于左半部分；否则位于右半部分，然后进一步缩小区间查找即可。

相关文章