数据结构-树状数组(二叉索引树)

发表于 分类于
本文字数： 3.7k 阅读时长 ≈ 3 分钟

概述

树状数组 (二叉索引树) 是一种用以维护区间信息 的数据结构。它具有实现简单、操作时间复杂度常数低于线段树等优点，但是它的适用范围小于线段树。

其结构图大致如下：

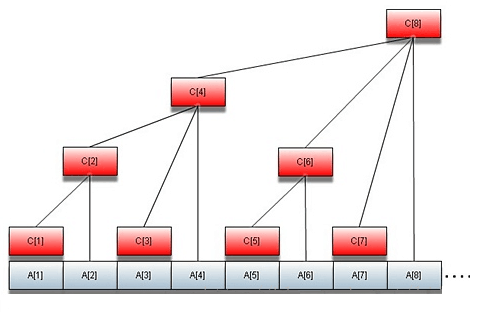
图一：树状数组

树状数组常用于求取指定区间元素之和，故而我们以此为引，讲述树状数组的思想。

假定存在一个数组 $A = [a_1, a_2, \dots, a_n]$ ，其上有两种操作：求取指定区间 $[fromIndex, toIndex]$ 元素之和、动态修改指定位置 $index$ 所在元素。我们很容易想到如下两种方案以满足这两种操作：

  1. 基于普通数组

    直接在该数组之上执行这两种操作。对于第一个操作而言，遍历指定区间，求和各元素，其时间复杂度为 $O(N)$；对于第二个操作，直接修改指定位置元素，其时间复杂度为 $O(1)$ 。

  2. 基于前缀数组

    将该数组转换为前缀数组 $prefix[]$ 以执行这两种操作。对于第一种操作而言，$prefix(toIndex) - prefix(fromIndex - 1)$ 即为指定区间元素之和，其时间复杂度为 $O(1)$；对于第二种操作，由于该位置之后的前缀元素都涉及加和该元素，故而需修改区间 $[index, prefix.length - 1]$ 内的所有元素，其时间复杂度为 $O(N)$ 。

从上述描述中，可以看到：两种方案各有优缺点，一种操作的时间复杂度极低，另一种操作的时间复杂度极高。对于树状数组而言，它可保证两种操作的时间复杂度均为 $O(log^N)$，这一点通过 “分层构造前缀和” 而做到。

树状数组其本质是一个数组，只不过基于数组索引的二进制位将数组逻辑映射为一棵树。我们首先介绍若干概念：

  1. $lowBit(index)$

    $lowBit(index)$ 定义为非负整数 $index$ 在二进制位表示下 “最低位的 $1$ 及其后所有的 $0$ “ 构成的数值。

    举例：$lowBit(24) = lowBit(0b00011000) = 0b1000 = 8$ 。

  2. $rangSum(index)$

    $rangSum(index)$ 定义为当前位置开始前 $i$ 个数之和，其中 $i = 2^k$，$k$ 为 $index$ 的二进制位表示下低位连续 $0$ 的个数。该定义同样可表示为当前位置开始前 $lowBit(index)$ 个数之和。

    举例：$rangSum(24) = rangSum(0b00011000)$，其为当前位置 $24$ 开始前 $2^3 = 8$ 个数之和，即区间 $[17,24]$ 元素之和。

基于此二者概念，按照 $rangSum(index)$ 所覆区间范围，可将其抽象为一棵树，具体如图一所示。

如果修改指定位置所在元素，只要向上依次修改其对应父节点所在元素即可，这一点可基于 $lowBit(index)$ 实现。例如：$parent(5) = 5 + lowBit(5) = 6， parent(6) = 6 + lowBit(6) = 8$ 。

另外，我们还可容易计算 $prefix(index)$ (假定数组开始位置为 $1$)，同样以图一举例说明：

$$prefix(6) = rangSum(6) + rangSum(6 - lowBit(6)) = rangSum(6) + rangSum(4) = [5,6] + [1,4]$$

树状数组不仅可用于指定区间求和，还可用于指定区间求最大值、指定区间求最小值等操作，但是为叙述方便，上述均以指定区间求和为例进行解释。

结构

1
2
3
4
5
6
7
8
9
10
class BinaryIndexedTree<E> {
    // 树状数组
    private Object[] bitArr;
    // 合并函数
    private Merge<E> merger;
}

public interface Merge<E> {
    E merge(E o1, E o2);
}

对应到求取 $prefix(index)$，接口实现应当为 $merger = (o1, o2) -> o1 + o2$ 。

实现

辅助方法

  • $lowBit()$

    1
    2
    3
    public int lowBit(int index) {
        return index & (-index);
    }

    初始化

树状数组初始化有两种方式，在此一一叙述：

  1. 基于更新实现

    最初置 $bitArr$ 中元素均为 $0$，顺序使用 $update()$ 更新每位。这种做法的时间复杂度为 $O(Nlog^N)$，但是它揭示了树状数组可在尾部插入元素这一事实。

  2. 直接遍历实现

    首先置 $bitArr$ 中元素均为元素数组对应元素，然后顺序遍历该数组，当遍历到某一个位置时，将当前元素合并到其父节点所在元素之中即可。这种做法的时间复杂度为 $O(N)$。代码实现中使用的便是这种做法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public BinaryIndexedTree(E[] arr, Merge<E> merger) {
    // 相比于原始数组而言，树状数组元素需后移一位。
    this.bitArr = new Object[arr.length + 1];
    this.merger = merger;

    for (int i = 1; i < this.bitArr.length; i++) {
        this.bitArr[i] = arr[i - 1];
    }

    for (int i = 1; i < this.bitArr.length; i++) {
        int j = i + lowBit(i);
        if (j < this.bitArr.length) {
            this.bitArr[j] = this.merger.merge((E) this.bitArr[j], (E) this.bitArr[i]);
        }
    }
}

查询

  • 查询指定区间 $[0,index]$ 值

    该值可以是区间元素之和、区间最大值、区间最小值。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    public E query(int index) {
        // bitArr中元素均后移一位，故而需有此操作。
        index++;
        // 输入非法，直接返回。
        if (index <= 0 || index >= this.bitArr.length) {
            return null;
        }

        E result = null;
        while (index != 0) {
            if (null == result) {
                result = (E) this.bitArr[index];
            } else {
                result = this.merger.merge(result, (E) this.bitArr[index]);
            }
            index -= lowBit(index);
        }

        return result;
    }

    操纵

  • 为指定位置元素加上某一差值

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    public void update(int index, E delta) {
        // bitArr中元素均后移一位，故而需有此操作。
        index++;
        // 输入非法，直接返回。
        if (index <= 0 || index >= this.bitArr.length) {
            return ;
        }

        while (index < this.bitArr.length) {
            this.bitArr[index] = this.merger.merge((E) this.bitArr[index], delta);
            index += lowBit(index);
        }
    }

拓展

这里介绍一种类似的数据结构——ST表。

ST表常用于解决 可重复贡献问题 。它可实现 $O(Nlog^N)$ 内建表、$O(1)$ 内查询，但是无法动态修改。

可重复贡献问题：

对于运算 $opt$，如果满足 $x \ opt \ x = x $，则对应的区间查询就是一个可重复贡献问题。例如，区间最大值、区间最小值，但是区间求和就不是一个可重复贡献问题。

ST表其本质是基于倍增思想、动态规划构建的一张二维表格。这里以求取区间最大值为例。

我们规定：$A$ 为元素数组、$f[i][j]$ 表示区间 $[i,i + 2^j - 1]$ 内元素最大值。

初始化条件即为：$f[i][0] = A[i], i \in [0, A.length]$ 。

状态转换方程即为：$f[i][j] = max(f[i][j - 1],f[i + 2^{j - 1}][j - 1])$ 。

基于上面两个等式，即可构建这张表。表大小为 $O(Nlog^N)$，故而建表的时间复杂度亦是如此。

对于任意指定区间 $[L,R]$，区间内最大值即为 $max(f[L][k],f[R - 2^{k} + 1][k]), \ k= \lfloor log_2^{(R - L + 1)}\rfloor$ 。

该等式成立原因即在于：$2^{\lfloor log_2^{(R - L + 1)}\rfloor} >= (R - L + 1) / 2$。正因如此，从 $L$ 开始前向 $2^k$ 个元素对应区间与从 $R$ 开始后向 $2^k$ 个元素对应区间的并集一定等于 $[L,R]$，故而二者之间的最大值亦为区间 $[L,R]$ 的最大值。从中也可看出，$f[L][k]$ 与 $f[R - 2^{k} + 1][k]$ 所覆盖区间是有重叠的，这也正是 “ST表只能解决可重复贡献问题” 的原因。

相关文章