数据结构-线段树

发表于 分类于
本文字数： 3.1k 阅读时长 ≈ 3 分钟

概述

线段树 是一种用以维护区间信息 的数据结构，它可在 $O(log^N)$ 时间内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。

其结构图大致如下：

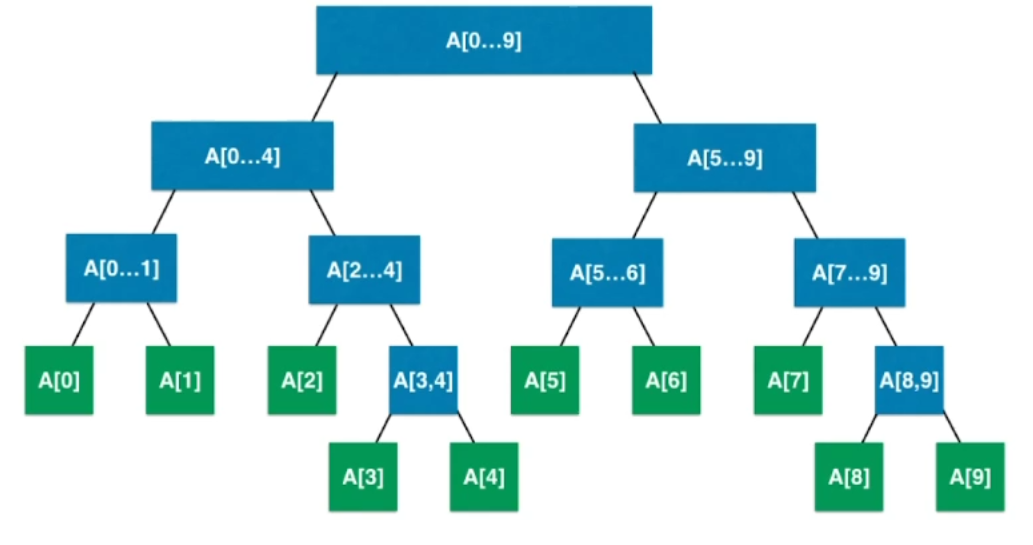
图一：线段树

关于线段树，以下几点需要注意：

  1. 线段树与区间树没有任何关系。
  2. 线段树不支持插入、删除操作。
  3. 叶节点保存数组中指定位置元素，非叶节点保存所在区间的值 (例如：区间最大值、区间最小值)。

结构

观察图一，发现其结构基本等同于一棵完全二叉树，故而我们使用数组加以实现。

1
2
3
4
5
6
7
8
9
10
11
12
class SegmentTree<E> {
    // 基础数组(从0开始)
    private Object[] elementData;
    // 线段树元素个数
    private int size;
    // 合并接口
    private Merge<E> merger;
}

public interface Merge<E> {
    E merge(E o1, E o2);
}

实现

辅助方法

  • 构建线段树

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    private void build(int treeIndex, int l, int r, E[] arr) {
        // 到达叶节点，直接赋值、返回即可。
        if (l >= r) {
            this.elementData[treeIndex] = arr[l];
            return ;
        }

        // 获取中间位置、左节点位置、右节点位置。
        int mid = (l + r) >> 1;
        int leftTreeIndex = treeIndex * 2 + 1;
        int rightTreeIndex = treeIndex * 2 + 2;
        
        // 递归构建左右子树，并更新当前节点所在区间值。
        build(leftTreeIndex, l, mid, arr);
        build(rightTreeIndex, mid + 1, r, arr);
        this.elementData[treeIndex] = merger.merge((E) this.elementData[leftTreeIndex], (E) this.elementData[rightTreeIndex]);
    }

  • 当前子树查询指定区间值

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    private E queryTree(int treeIndex, int l, int r, int left, int right) {
        // 满足查询区间，直接返回即可。
        if (l == left && r == right) {
            return (E) this.elementData[treeIndex];
        }
        
        // 获取中间位置、左节点位置、右节点位置。
        int mid = (l + r) >> 1;
        int leftTreeIndex = treeIndex * 2 + 1;
        int rightTreeIndex = treeIndex * 2 + 2;
        
        // 查询区间在左子树所在区间之中，则在左子树中进行查询。
        if (mid >= right) {
            return queryTree(leftTreeIndex, l, mid, left, right);
        } else if (mid < left) {
            // 查询区间在右子树所在区间之中，则在右子树中进行查询。
            return queryTree(rightTreeIndex, mid + 1, r, left, right);
        } else {
            // 查询区间横贯左右子树所在区间，则在左右子树中进行相应查找，然后合并查询结果即可。
            return merger.merge(queryTree(leftTreeIndex, l, mid, left, mid), queryTree(rightTreeIndex, mid + 1, r, mid + 1, right));
        }
    }

  • 当前子树更新指定位置元素内容

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    private void updateTree(int treeIndex, int l, int r, int index, E value) {
        // 找到指定位置元素，直接修改即可。
        if (l >= r) {
            this.elementData[treeIndex] = value;
            return ;
        }
        
        // 获取中间位置、左节点位置、右节点位置。
        int mid = (l + r) >> 1;
        int leftTreeIndex = treeIndex * 2 + 1;
        int rightTreeIndex = treeIndex * 2 + 2;
        
        // 如果指定位置在左子树所在区间之中，则在左子树中进行修改，反之则在右子树中进行修改。
        if (mid >= index) {
            updateTree(leftTreeIndex, l, mid, index, value);
        } else {
            updateTree(rightTreeIndex, mid + 1, r, index, value);
        }

        // 更新当前节点所在区间值。
        this.elementData[treeIndex] = merger.merge((E) this.elementData[leftTreeIndex], (E) this.elementData[rightTreeIndex]);
    }

    初始化

1
2
3
4
5
6
7
8
public SegmentTree(E[] arr, Merge<E> merger) {
    // 根据相关推理，如果数组长度为N,对应线段树最多需要4N空间。
    this.elementData = new Object[4 * arr.length];
    this.size = arr.length;
    this.merger = merger;

    build(0, 0, this.size - 1, arr);
}

查询

  • 查询指定区间的值

    1
    2
    3
    4
    5
    6
    7
    public E query(int left,int right) {
        if (left < 0 || right >= this.size || left < right) {
            // 输入非法，直接返回。
            return null;
        }
        return queryTree(0, 0, this.size - 1, left, right);
    }

    操纵

  • 更新指定位置元素内容

    1
    2
    3
    4
    5
    6
    7
    public void update(int index, E value) {
        if (index < 0 || index >= this.size) {
            // 输入非法，直接返回。
            return ;
        }
        updateTree(0, 0, this.size - 1, index, value);
    }

  • 更新指定区间内容

    更新指定区间内容涉及更新具体操作，我们在此规定情景，并指明更新区间内容的方法。

    我们规定情景如下：

    1. 非叶节点保存所在区间元素的最大值。
    2. 更新操作为：为指定区间所有元素均加上某一常数。

    搜索找到区间内所有元素，并为其加上某一常数，这样即可达到更新目的。显而易见，这种方式的时间复杂度为 $O(N)$。为使得更新操作复杂度降为 $O(log^N)$，线段树引入懒更新。

    首先在节点结构中引入 mark 字段 (其意义：为左右子树各元素需要加上的常数)。进行更新操作时，我们找到需要更新区间对应的节点，然后仅更新这些节点的所在区间值和 mark 字段。后续查询到某个节点时，如果该节点的 mark 字段非零，表明左右子树需要更新，则更新左右子树根节点的信息 (如果左右子树根节点被访问，则进一步更新对应节点的左右子树根节点，直至到达叶节点)。

相关文章