数据结构-块状链表

概述

块状链表 是一种比较中庸的数据结构。它将 “分块思想” 应用于链表之中，从而整合了线性表与链表的优缺点，使得其上操作的时间复杂度均为 $O(\sqrt{N})$。

其结构图大致如下：

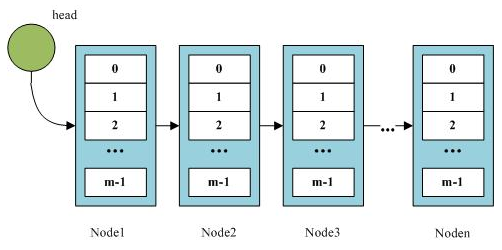
假定数据总量为 $N$，将这些数据均分为 $\sqrt{N}$ 块，块内数据使用线性表进行存储，块间使用引用进行链接，如此组织便是块状链表。对块状链表操作时，首先需要花费 $O(\sqrt{N})$ 时间定位到块，随后花费 $O(\sqrt{N})$ 在块内执行操作，故而操作的时间复杂度为 $O(\sqrt{N})$。

“分块思想” 其本质为一棵仅有三层的多叉树，其结构如图所示。

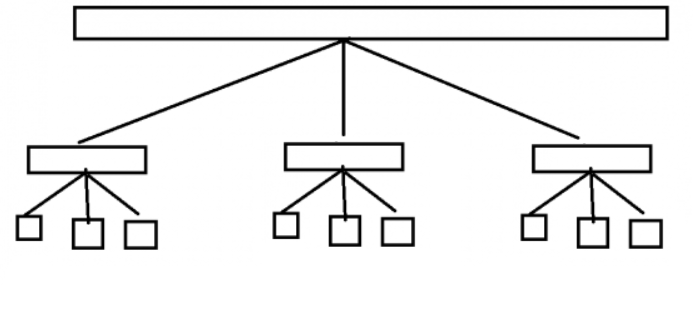
结构

块状链表中存储的数据量大小通常是未知的，故而通常需要预估数据量大小以指定块大小。

class BlockList<E> {
    // 节点结构
    private static class Node<E> {
        // 块内元素个数
        int blockSize;
        // 块内线性表
        Object[] blockArr;
        // 后继块
        Node<E> next;

        public Node() {
            this.blockSize = 0;
            this.blockArr = new Object[BlockList.BLOCK_SIZE];
            this.next = null;
        }
    }

    // 块大小
    public static final int BLOCK_SIZE = 4;
    // 链首
    private Node<E> head;
}

实现

块状链表中块大小及块个数决定着操作的时间复杂度，因此每次操作后需要对此二者进行一定调整。

辅助方法

• 相邻块合并

  private void unionBlock(Node<E> e1, Node<E> e2) {
      // 合并线性表中元素
      for (int i = 0; i < e2.blockSize; i++) {
          e1.blockArr[e1.blockSize + i] = e2.blockArr[i];
      }
  
      // 更新相关字段
      e1.blockSize += e2.blockSize;
      e1.next = e2.next;
  }

• 维护链形态

  private void maintain() {
      Node node = this.head;
      while (null != node && null != node.next) {
          // 如果相邻块中元素个数小于指定的块大小，则需要进行合并。
          if (node.blockSize + node.next.blockSize < BlockList.BLOCK_SIZE) {
              unionBlock(node, node.next);
              continue;
          }
          node = node.next;
      }
  }

• 在指定位置处分割块

  private void splitBlock(Node<E> e1, int index) {
      // index非法，直接返回即可。
      if (index < 0 || index > e1.blockSize) {
          return ;
      }
  
      // 创建新块，并调整引用。
      Node<E> e2 = new Node<>();
      e2.next = e1.next;
      e1.next = e2;
      
      // 分割线性表中元素。
      for (int i = index; i < e1.blockSize; i++) {
          e2.blockArr[i - index] = e1.blockArr[i];
          e2.blockSize++;
          e1.blockArr[i] = null;
      }
  
      e1.blockSize = index;
  }

  初始化

public BlockList() {
    head = new Node<>();
}

查询

• 查询指定位置的元素

  public E get(int index) {
      Node<E> node = this.head;
      while (null != node) {
          if (index >= node.blockSize) {
              index = index - node.blockSize;
              node = node.next;
          } else {
              break;
          }
      }
  
      return null == node ? null : (E) node.blockArr[index];
  }

  操纵

• 块状链表中添加元素

  我们假定块中元素个数始终小于指定的块大小。

  public void insert(int index, E item) {
      // 寻找待插入块及待插入位置
      Node<E> node = this.head;
      while (true) {
          if (index > node.blockSize) {
              if (null != node.next) {
                  index = index - node.blockSize;
                  node = node.next;
              } else {
                  // 插入位置有误，直接返回即可。
                  return ;
              }
          } else {
              break;
          }
      }
  
      // 插入元素至指定位置。
      for (int i = node.blockSize; i > index; i--) {
          node.blockArr[i] = node.blockArr[i - 1];
      }
      node.blockArr[index] = item;
      node.blockSize++;
      
      // 插入元素后，如果块已满，则需要从中部分割块。
      if (node.blockSize == BlockList.BLOCK_SIZE) {
          splitBlock(node, BlockList.BLOCK_SIZE / 2);
      }
      
      maintain();
  }

• 块状链表中删除元素

  public void delete(int index) {
      // 寻找待删除块及待删除位置
      Node<E> node = this.head;
      while (null != node) {
          if (index >= node.blockSize) {
              index = index - node.blockSize;
              node = node.next;
          } else {
              break;
          }
      }
  
      // 没有找到，直接返回即可。
      if (null == node) {
          return;
      }
  
      // 删除指定元素。
      for (int i = index; i < node.blockSize - 1; i++) {
          node.blockArr[i] = node.blockArr[i + 1];
      }
      node.blockSize--;
      node.blockArr[node.blockSize] = null;
  
      maintain();
  }