数据结构-配对堆
概述
配对堆 是斐波那契堆的简化版本。其不仅具有斐波那契堆那般优秀的操作复杂度,同时易于实现。
其结构图大致如下:
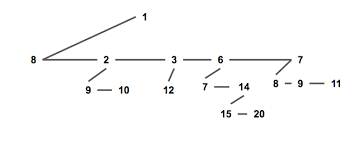
相比斐波那契堆实现而言,配对堆主要在如下两个方面进行优化:1. 优化节点结构,节省节点所需内存空间;2. 降低各种操作的编码复杂度。
结构
配对堆中节点除保存具体元素外,仅需保存三个引用即可。
1 | class PairHeap<E> { |
实现
辅助方法
重置
pre与nextSibling引用重置此二者,保证配对堆合法(配对堆根节点的
pre与nextSibling应当为null)。1
2
3
4private void reset(Node<E> root) {
root.pre = null;
root.nextSibling = null;
}合并两个配对堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27private Node<E> merge(Node<E> root1, Node<E> root2) {
// 只要一者为空,直接返回另一者即可。
if (null == root1) {
return root2;
} else if (null == root2) {
return root1;
}
// 如果前者大于后者,则应交换二者。
if (comparator.compare(root1.item, root2.item) > 0) {
return merge(root2, root1);
}
// 保证配对堆合法。
reset(root1);
reset(root2);
// 调整相关引用。
root2.nextSibling = root1.leftChild;
if (null != root1.leftChild) {
root1.leftChild.pre = root2;
}
root1.leftChild = root2;
root2.pre = root1;
return root1;
}合并一个节点的所有兄弟节点
合并兄弟节点的顺序是有要求的:所有兄弟节点按顺序从前往后两两配对进行合并,随后从后往前依次合并即可。只有按照此种方式进行合并,才能够保证 $O(log^N)$ 的复杂度界限。
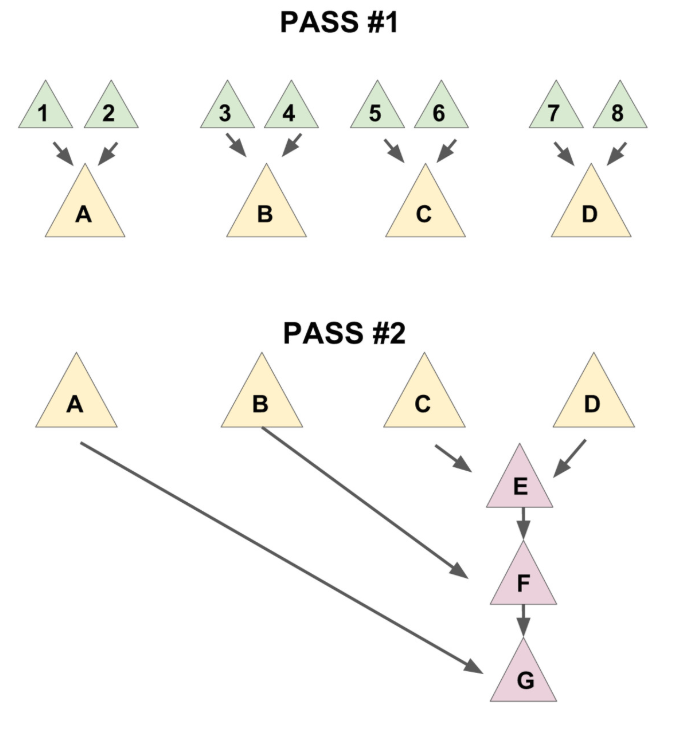
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16private Node<E> merges(Node<E> root) {
// 当前节点为空,或者没有任何儿子节点,直接返回该节点即可。
if (null == root || null == root.nextSibling) {
if (null != root) {
reset(root);
}
return root;
}
// 取出前两个兄弟节点
Node<E> first = root;
Node<E> second = first.nextSibling;
root = second.nextSibling;
return merge(merge(first, second), merges(root));
}初始化
1 | public PairHeap(Comparator<? super E> comparator) { |
查询
查询最小元素
1
2
3public E getMin() {
return null == this.root ? null : this.root.item;
}操纵
配对堆合并
直接合并即可。
1
2
3
4public void merge(PairHeap<E> pairHeap) {
this.root = merge(this.root, pairHeap.root);
pairHeap.root = null;
}配对堆中添加元素
将待添加元素包装为一个配对堆,然后合并两个堆即可。
1
2
3
4public void add(E item) {
Node<E> node = new Node<>(item, null, null, null);
this.root = merge(this.root, node);
}配对堆中删除最小元素
合并根节点的所有儿子节点,然后将合并结果赋值给
this.root即可。1
2
3
4
5
6
7public void deleteMin() {
if (null == this.root) {
return ;
}
this.root = merges(this.root.leftChild);
}配对堆中指定节点降低元素值
将指定节点所表示的配对堆从当前配对堆中剔除,合并两个配对堆即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25public void decreaseKey(Node<E> node, E item) {
// 如果修改值大于当前值,则直接返回。
if (comparator.compare(node.item, item) < 0) {
return ;
}
node.item = item;
// 指定节点为根节点,直接返回即可。
if (null == node.pre) {
return ;
}
// 从配对堆中剔除指定节点所表示的子配对堆。
// 当前节点为第一个儿子节点
if (node.pre.leftChild == node) {
node.pre.leftChild = node.nextSibling;
node.nextSibling.pre = node.pre;
} else {
node.pre.nextSibling = node.nextSibling;
node.nextSibling.pre = node.pre;
}
this.root = merge(this.root, node);
}配对堆中删除指定节点
通过降低元素值方式使指定节点称为根节点,然后删除根节点即可。
1
2
3
4public void delete(Node<E> node) {
decreaseKey(node, this.root.item);
deleteMin();
}
相关文章