数据结构-k-d树

发表于 分类于
本文字数： 11k 阅读时长 ≈ 10 分钟

概述

k-d 树 是在 $k$ 维欧几里德空间中组织点的一种数据结构。其可应用于多种场合，例如多维键值查询、范围查询、最近邻搜索。

其结构图大致如下：

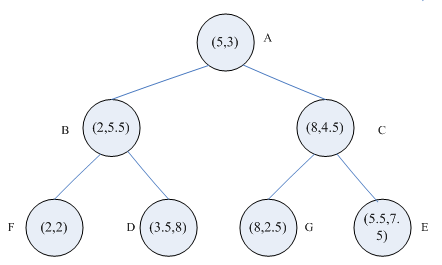
图一：k-d树

k-d 树看似复杂，其实原理十分简单。本文之中，我们便以 1-d树、2-d树为例说明 k-d树的原理。

  • 1-d 树

    1-d 树是在一维空间 (直线) 中组织点的一种数据结构，其实就是二叉查找树。观察该种数据结构，可以发现：它借由某个点将直线划分为两部分，前半部分直线中点所表示的数据均小于该点所表示的数据，后半部分直线中点所表示的数据均大于该点所表示的数据。通过这种有序组织数据，可避免无效的搜索，从而降低查询操作的时间复杂度。

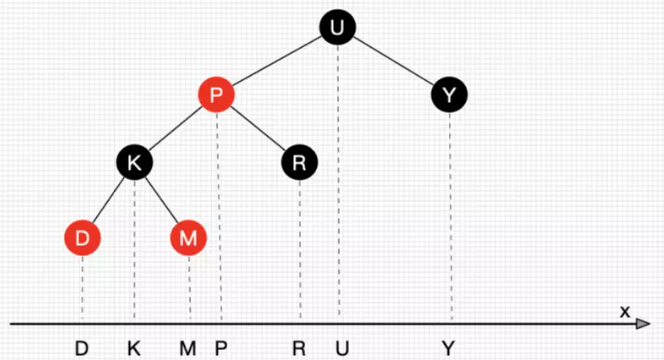
    图二：1-d树映射于直线

  • 2-d 树

    2-d 树是在二维空间 (平面) 中组织点的一种数据结构。为降低查询操作的时间复杂度，我们同样需要有序组织数据。按照升维的一般规律，我们可以这样设想该种数据结构 (实际上也是这么做的)：它借由某条直线将平面划分为两部分，前半部分平面中点所表示的数据均小于该条直线上点所表示的数据，后半部分平面中点所表示的数据均大于该条直线上点所表示的数据。

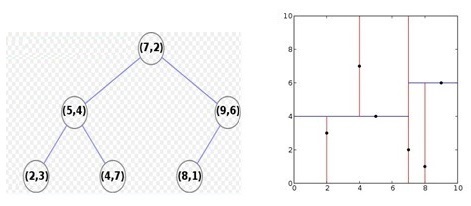
    图三：2-d树映射于平面

从上面例子中，可以窥知：k-d 树会借由某种方式将 $k$ 维空间划分为两部分，并以此有序组织数据，从而更为快速地完成数据查询。

考虑到 2-d树易于实现，因此本文仅涉及 2-d树的代码实现。上面例子仅说明了 2-d树的原理，接下来通过几个问题详细描述一下 2-d树的实现方式。

  1. 如何表示这条直线？

    对于一个 $k$ 维空间，仅以某一维度的数据值进行排序，这样便会将该空间划分为两部分。对于二维空间而言，其将映射为一条直线；对于三维空间而言，其将映射为一个平面。

  2. 如何选择维度？

    通常有两种维度选择方式：

    • 按原始维度顺序依次指定为排序维度，循环往复。对于 2-d树而言，树的第一层按照 $x$ 轴进行排序，树的第二层按照 $y$ 轴进行排序，树的第三层按照 $x$ 轴进行排序，$\dots$。
    • 对初始数据集计算各维度方差，方差大者在前，方差小者在后，以此构建一个维度顺序。按此维度顺序依次指定为排序维度，循环往复。假定根据构建的维度顺序为 $(y,x)$，那么对于 2-d树而言，树的第一层按照 $y$ 轴进行排序，树的第二层按照 $x$ 轴进行排序，树的第三层按照 $y$ 轴进行排序，$\dots$。

  3. 如何选择这条直线？

    假定对数据集中所有数据按照排序维度进行排序，排序结果位于中间的那个多维数据即为划分点。指定当前划分点为根结点，如果一个多维数据的排序维度值小于划分点的排序维度值，那么其将位于左子树之中，否则其将位于右子树之中。

k-d树查询操作的最好时间复杂度为 $O(log^N)$，最坏时间复杂度为 $O(N^{1 - 1/k})$。如果数据维度较低，综合考虑时间复杂度及编程复杂度，应当选择使用 k-d树，；如果数据维度较高，应当着重考虑时间复杂度，此时需选择使用 R树。

结构

为支撑众多功能，2-d树结构比较复杂。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
class KDTree {
    // 位置坐标
    public static class Point implements Cloneable {
        double x;
        double y;

        public Point(double x, double y) {
            this.x = x;
            this.y = y;
        }

        // 与指定坐标的曼哈顿距离
        public double distance(Point point) {
            return Math.abs(this.x - point.x) + Math.abs(this.y - point.y);
        }

        // 比较函数
        public int compareTo(Point point, boolean dimension) {
            if (dimension) {
                return Double.compare(this.x, point.x);
            } else {
                return Double.compare(this.y, point.y);
            }
        }

        // 比较器
        public Comparator comparator(boolean dimension) {
            if (dimension) {
                return (o1, o2) -> Double.compare(((Point) o1).x, ((Point) o2).x);
            } else {
                return (o1, o2) -> Double.compare(((Point) o1).y, ((Point) o2).y);
            }
        }

        // 克隆
        public Point clone() {
            return new Point(this.x, this.y);
        }
    }
    
    // 节点结构
    private static class Node {
        // 具体元素
        Point item;
        // 节点所覆盖区域左下角的位置坐标
        Point leftBottom;
        // 节点所覆盖区域右上角的位置坐标
        Point rightUp;
        // 左儿子
        Node left;
        // 右儿子
        Node right;

        public Node(Point item, Point leftBottom, Point rightUp, Node left, Node right) {
            this.item = item;
            this.leftBottom = leftBottom;
            this.rightUp = rightUp;
            this.left = left;
            this.right = right;
        }

        // 更新节点所覆盖区域
        public void maintain() {
            this.leftBottom.x = Math.min(Math.min(this.left.leftBottom.x, this.right.leftBottom.x), this.item.x);
            this.leftBottom.y = Math.min(Math.min(this.left.leftBottom.y, this.right.leftBottom.y), this.item.y);
            this.rightUp.x = Math.max(Math.max(this.left.rightUp.x, this.right.rightUp.x), this.item.x);
            this.rightUp.y = Math.max(Math.max(this.left.rightUp.y, this.right.rightUp.y), this.item.y);
        }

        // 指定坐标与当前节点所覆盖区域的最近曼哈顿距离
        public double minDistance(Point point) {
            // 如果当前节点为空节点，直接返回无穷大。
            if (KDTree.nullNode == this) {
                return KDTree.INF;
            }

            if ((this.leftBottom.x < point.x && point.x < this.rightUp.x)
                    && (this.leftBottom.y < point.y && point.y < this.rightUp.y)) {
                return 0;
            }

            Point leftUp = new Point(this.leftBottom.x, this.rightUp.y);
            Point rightBottom = new Point(this.rightUp.x, this.leftBottom.y);
            return Math.min(Math.min(this.leftBottom.distance(point), this.rightUp.distance(point)),
                    Math.min(leftUp.distance(point), rightBottom.distance(point)));
        }

        // 指定坐标与当前节点所覆盖区域的最远曼哈顿距离
        public double maxDistance(Point point) {
            // 如果当前节点为空节点，直接返回负无穷大。
            if (KDTree.nullNode == this) {
                return -KDTree.INF;
            }

            Point leftUp = new Point(this.leftBottom.x, this.rightUp.y);
            Point rightBottom = new Point(this.rightUp.x, this.leftBottom.y);
            return Math.max(Math.max(this.leftBottom.distance(point), this.rightUp.distance(point)),
                    Math.max(leftUp.distance(point), rightBottom.distance(point)));
        }
    }
    
    // 状态（大小堆之用）
    private static class Status implements Comparable {
        Point point;
        double distance;

        public Status(Point point, double distance) {
            this.point = point;
            this.distance = distance;
        }

        @Override
        public int compareTo(Object o) {
            return Double.compare(this.distance, ((Status) o).distance);
        }
    }
    
    // 无穷值
    public static int INF = 0x3f3f3f3f;
    // 空节点（方便编码）
    public static Node nullNode = new Node(null, new Point(KDTree.INF, KDTree.INF),
            new Point(-KDTree.INF, -KDTree.INF), null, null);
    // 根节点
    private Node root;
}

实现

辅助方法

  • 基于 arr[l,r) 间元素、按照指定维度构建 KDTree

    该代码实现需要注意两部分：

    1. 代码实现中直接排序 arr[l,r) 中全部元素，其时间复杂度为 $O(nlog^n)$。实际上没有必要这样做，只要找到一个元素将其放置中间位置，使得前面元素均小于它，后面元素均大于它即可。这一操作的平均时间复杂度为 $O(n)$ (具体实现可参见 C++ 中的 nth_element 函数)。故而构建 KDTree 的时间复杂度为 $O(Nlog^N)$ 。
    2. 构建节点时，item、leftBottom 与 rightUp 应当是互相独立的，故而其无法引用同一对象，应当引用内容相同的对象。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    // dimension为true,表示应当按 x轴排序，反之应当按 y轴排序。后面同此，故不再赘述。
    private Node build(int l, int r, Point[] arr, boolean dimension) {
        // 基于零个元素构建KDTree，直接返回空节点即可。
        if (l >= r) {
            return KDTree.nullNode;
        }

        // 排序这部分元素
        Arrays.sort(arr, l, r, arr[l].comparator(dimension));
        // 获取中间位置
        int mid = (l + r) >> 1;

        // 构建节点及其子树
        Node root = new Node(arr[mid], arr[mid].clone(), arr[mid].clone(), null, null);
        root.left = build(l, mid, arr, !dimension);
        root.right = build(mid + 1, r, arr, !dimension);

        // 更新节点所覆盖区域
        root.maintain();
        return root;
    }

  • 当前子树中获取KNN

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    private void KNNTree(Point point, int k, PriorityQueue<Status> priorityQueue, Node root) {
        // 空子树中一定不存在，直接返回即可。
        if (KDTree.nullNode == root) {
            return ;
        }

        // 获取当前子树根节点与指定节点的曼哈顿距离
        double distance = root.item.distance(point);
        
        // 如果搜索到的邻居节点数不足，则直接插入。如果搜索到的邻居节点数已满，但是当前子树根节点与指定节点的曼哈顿距离小于大顶堆堆顶元素，则应当移除堆顶元素，并将该曼哈顿距离置于堆中。
        if (priorityQueue.size() < k || distance < priorityQueue.peek().distance) {
            if (priorityQueue.size() == k) {
                priorityQueue.remove();
            }
            priorityQueue.add(new Status(root.item, distance));
        }

        double leftDistance = root.left.minDistance(point);
        double rightDistance = root.right.minDistance(point);

        if (leftDistance < rightDistance) {
            KNNTree(point, k, priorityQueue, root.left);
            // 如果搜索到的邻居节点数不足或者邻居节点数已足但是右子树最近距离小于大顶堆堆顶元素，就需要搜索右子树。
            if (priorityQueue.size() < k || rightDistance < priorityQueue.peek().distance) {
                KNNTree(point, k, priorityQueue, root.right);
            }
        } else {
            KNNTree(point, k, priorityQueue, root.right);
            // 如果搜索到的邻居节点数不足或者邻居节点数已足但是左子树最近距离小于大顶堆堆顶元素，就需要搜索左子树。
            if (priorityQueue.size() < k || leftDistance < priorityQueue.peek().distance) {
                KNNTree(point, k, priorityQueue, root.left);
            }
        }
    }

  • 当前子树中获取KNF

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    private void KNFTree(Point point, int k, PriorityQueue<Status> priorityQueue, Node root){
        // 空子树中一定不存在，直接返回即可。
        if (KDTree.nullNode == root) {
            return ;
        }
    	
        // 获取当前子树根节点与指定节点的曼哈顿距离
        double distance = root.item.distance(point);
        
        // 如果搜索到的邻居节点数不足，则直接插入。如果搜索到的邻居节点数已满，但是当前子树根节点与指定节点的曼哈顿距离大于小顶堆堆顶元素，则应当移除堆顶元素，并将该曼哈顿距离置于堆中。
        if (priorityQueue.size() < k || distance > priorityQueue.peek().distance) {
            if (priorityQueue.size() == k) {
                priorityQueue.remove();
            }
            priorityQueue.add(new Status(root.item, distance));
        }

        double leftDistance = root.left.minDistance(point);
        double rightDistance = root.right.minDistance(point);
        
        if (leftDistance > rightDistance) {
            KNFTree(point, k, priorityQueue, root.left);
            // 如果搜索到的邻居节点数不足或者邻居节点数已足但是右子树最远距离大于小顶堆堆顶元素，就需要搜索右子树。
            if (priorityQueue.size() < k || rightDistance > priorityQueue.peek().distance) {
                KNFTree(point, k, priorityQueue, root.right);
            }
        } else {
            KNFTree(point, k, priorityQueue, root.right);
            // 如果搜索到的邻居节点数不足或者邻居节点数已足但是左子树最远距离大于小顶堆堆顶元素，就需要搜索左子树。
            if (priorityQueue.size() < k || leftDistance > priorityQueue.peek().distance) {
                KNFTree(point, k, priorityQueue, root.left);
            }
        }
    }

  • 当前子树中获取具有指定维度最小值的节点

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    private Node findminTree(Node root, boolean dimension, boolean specDim, Node min) {
        // 当前子树为空，直接返回传入的min。
        if (KDTree.nullNode == root) {
            return min;
        }

        // 如果min为空节点，或者当前子树根节点指定维度值小于min，则赋值min为当前子树根节点。
        if (KDTree.nullNode == min || root.item.compareTo(min.item, specDim) < 0) {
            min = root;
        }

        // 如果当前维度为指定维度，只需在左子树中查找即可。否则左右子树均需查找。
        if (dimension == specDim) {
            return findminTree(root.left, !dimension, specDim, min);
        } else {
            Node leftMin = findminTree(root.left, !dimension, specDim, min);
            Node rightMin = findminTree(root.right, !dimension, specDim, min);

            return leftMin.item.compareTo(rightMin.item, specDim) < 0 ? leftMin : rightMin;
        }
    }

  • 当前子树中添加指定元素

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    private Node addTree(Point point, Node root, boolean dimension) {
        // 当前子树为空，直接创建节点并返回即可。
        if (KDTree.nullNode == root) {
            return new Node(point, point.clone(), point.clone(), KDTree.nullNode, KDTree.nullNode);
        }

        // 待添加元素小于当前子树根节点值，表明应插入于左子树之中。
        if (root.item.compareTo(point,dimension) > 0) {
            root.left = addTree(point, root.left, !dimension);
        } else {
            root.right = addTree(point, root.right, !dimension);
        }

        // 更新节点所覆盖区域
        root.maintain();
        return root;
    }

  • 当前子树中删除指定元素

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    private Node deleteTree(Point point, Node root, boolean dimension) {
        // 当前子树为空，直接返回即可。
        if (KDTree.nullNode == root) {
            return KDTree.nullNode;
        }

        // 当前子树根节点并非待删除元素，根据维度顺序，在左右子树中删除即可。
        if (root.item.x != point.x || root.item.y != point.y) {
            if (root.item.compareTo(point, dimension) > 0) {
                root.left = deleteTree(point, root.left, !dimension);
            } else {
                root.right = deleteTree(point, root.right, !dimension);
            }
        } else {
            // 表明当前子树根节点就是待删除元素
            // 当前子树右子树不为空，将当前子树根节点的元素值与其后继节点元素值交换，然后删除其后继节点即可。
            if (KDTree.nullNode != root.right) {
                root.item = findminTree(root.right, !dimension, dimension, KDTree.nullNode).item;
                root.right = deleteTree(root.item, root.right, !dimension);
            } else if (KDTree.nullNode != root.left){
                // 当前子树左子树不为空，将当前子树根节点的元素值与左子树中具有指定维度最小值的节点的元素值交换，然后删除左子树中具有指定维度最小值的节点，最后为保证有序，将当前子树的左右子树交换即可。
                root.item = findminTree(root.left, !dimension, dimension, KDTree.nullNode).item;
                root.left = deleteTree(root.item, root.left, !dimension);
                root.right = root.left;
                root.left = KDTree.nullNode;
            } else {
                // 左右子树为空，删除该节点后，应当返回空节点。
                return KDTree.nullNode;
            }
        }

        // 更新节点所覆盖区域
        root.maintain();
        return root;
    }

初始化

1
2
3
public KDTree(Point[] arr) {
    this.root = build(0, arr.length, arr, true);
}

查询

  • KNN（K邻近）

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    public void KNN(Point point, int k) {
        // 构建大顶堆
        PriorityQueue<Status> priorityQueue = new PriorityQueue<>(new Comparator<Status>() {
            @Override
            public int compare(Status o1, Status o2) {
                return Double.compare(o2.distance, o1.distance);
            }
        });

        KNNTree(point, k, priorityQueue, this.root);

        System.out.println("KNN: ");
        while (!priorityQueue.isEmpty()) {
            Status tmp = priorityQueue.remove();
            System.out.println("X: " + tmp.point.x + ",Y: " + tmp.point.y);
        }
    }

  • KNF（K最远）

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    public void KNF(Point point, int k) {
        // 构建小顶堆
        PriorityQueue<Status> priorityQueue = new PriorityQueue<>(new Comparator<Status>() {
            @Override
            public int compare(Status o1, Status o2) {
                return Double.compare(o1.distance, o2.distance);
            }
        });

        KNFTree(point, k, priorityQueue, this.root);
        System.out.println("KNF: ");
        while (!priorityQueue.isEmpty()) {
            Status tmp = priorityQueue.remove();
            System.out.println("X: " + tmp.point.x + ",Y: " + tmp.point.y);
        }
    }

    操纵

  • KDTree 中添加元素

    1
    2
    3
    public void add(Point point) {
        this.root = addTree(point, this.root, true);
    }

  • KDTree 中删除元素

    1
    2
    3
    public void delete(Point point) {
        this.root = deleteTree(point, this.root, true);
    }
相关文章