数据结构-跳跃表

发表于 分类于
本文字数： 5.6k 阅读时长 ≈ 5 分钟

概述

跳跃表 是一种基于链表实现的数据结构。它具有实现简单、查找性能媲美甚至优于平衡树、内存占用较少等特点。

其结构图大致如下：

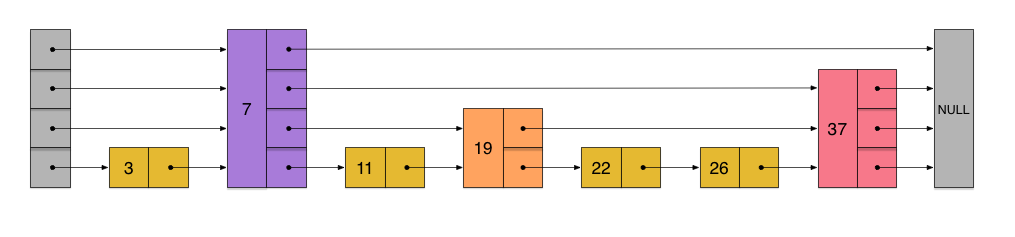
图一：跳跃表

对于排序数组而言，基于二分思想可将查找操作的时间复杂度降为 $O(log^N)$；而对于排序链表而言，由于其节点只保存后继节点的引用信息，故而其查找操作的时间复杂度只能是 $O(N)$。受 “空间换时间” 思想的启发，我们会产生这样一种想法：如果一部分节点不仅保存后继节点的引用信息，而且保存后继节点的后继节点的引用信息，甚至于保存后继节点的后继节点的后继节点的引用信息，那么一定可以降低查询操作的时间复杂度。最终我们可以得到这样一种理想的跳跃表：第零层级存在所有节点，第一层级只有 $1/2$ 的节点，而且是均匀间隔的，第二层级只有 $1/4$ 的节点，同样是均匀间隔的，以此类推，直至最高层级仅有两个节点。这种跳跃表共有 $log^N$ 层，故而其查询操作的时间复杂度为 $O(log^N)$。

图二：理想的跳跃表

理想的跳跃表存在一个非常大的问题：结构过于严谨，致使插入操作和删除操作非常复杂。为简化操作复杂度，不确定性跳跃表和确定性跳跃表应运而生。前者基于概率模拟理想的跳跃表，故而其查询操作的平均时间复杂度为 $O(log^N)$，后者基于结构限制模拟理想的跳跃表，故而其查询操作的时间复杂度为 $O(log^N)$ 。

因为确定性跳跃表并不常用，故而本文着重于不确定性跳跃表的代码实现，仅在 拓展 一节简要介绍确定性跳跃表。

结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class SkipList<E> {
    // 节点结构
    private static class Node<E> {
        // 具体元素
        E item;
        // 后继节点的引用数组
        Node<E>[] next;

        public Node(E item, int level) {
            this.item = item;
            this.next = new Node[level + 1];
        }
    }
    // 最大层级数
    private int maxLevel;
    // 概率参数，指定层级数之用
    private double p;
    // 当前跳跃表中最大层级数
    private int level;
    // 首节点
    private Node<E> head;
    // 随机函数，指定层级数之用
    private static Random random = new Random(System.currentTimeMillis());
    // 比较函数
    private final Comparator<? super E> comparator;
}

实现

辅助方法

  • 指定层级数

    跳跃表中指定节点层级数的方法十分有趣。最初设置层级数为零，如果随机数值小于指定的概率参数，且当前层级数小于指定的最大层级数，则层级数加一；反之当前层级数就是该节点的最终层级数。

    1
    2
    3
    4
    5
    6
    7
    private int randomLevel() {
        int level = 0;
        while (random.nextDouble() < this.p && level < this.maxLevel) {
            level++;
        }
        return level;
    }

    初始化

1
2
3
4
5
6
7
8
9
10
public SkipList(int maxLevel, double p, Comparator<? super E> comparator) {
    // 赋值相关参数。
    this.maxLevel = maxLevel;
    this.p = p;
    this.comparator = comparator;

    // 初始化相关参数
    this.head = new Node<>(null, this.maxLevel);
    this.level = 0;
}

查询

  • 查询指定元素是否存在

    从最高层级开始向前搜索，如果下一个节点元素值大于等于待查找元素值，则转向下一层级并向前搜索，依此而行，直至转向第零层级。如果第零层级不存在该值则查找失败，否则查找成功。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    public boolean search(E item) {
        // 栈，用于存放各个层级上最后一个小于待查找元素的节点。
        ArrayDeque<Node<E>> stack = new ArrayDeque<>();
        // 当前搜索节点
        Node<E> current = this.head;

        for (int i = this.maxLevel; i >= 0; i--) {
            // 当前层级之下当前节点的下一个节点存在，且值小于或等于待查找元素，则继续向前搜索。
            while (null != current.next[i] && comparator.compare(current.next[i].item, item) < 0) {
                current = current.next[i];
            }
            // 当前节点为当前层级之上最后一个小于或等于待查找元素的节点，故将其添加至栈中。
            stack.push(current);
        }

        // 第零层级当前搜索节点的下一个节点不存在或者节点元素值不等于待查找元素，则查找失败。
        if (null == current.next[0] || comparator.compare(current.next[0].item, item) != 0) {
            return false;
        }
        return true;
    }

    操纵

  • 跳跃表中添加元素

    插入过程与查询过程类似，只是需要从下往上依次插入待添加元素即可。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    public void add(E item) {
        // 栈，用于存放各个层级上最后一个小于待添加元素的节点。
        ArrayDeque<Node<E>> stack = new ArrayDeque<>();
        // 当前搜索节点
        Node<E> current = this.head;

        for (int i = this.maxLevel; i >= 0; i--) {
            // 当前层级之下当前节点的下一个节点存在，且值小于待添加元素，则继续向前搜索。
            while (null != current.next[i] && comparator.compare(current.next[i].item, item) < 0) {
                current = current.next[i];
            }
            // 当前节点为当前层级之上最后一个小于待添加元素的节点，故将其添加至栈中。
            stack.push(current);
        }

        // 指定层级数，同时更新当前跳跃表中最大层级数。
        int rLevel = randomLevel();
        if (rLevel > this.level) {
            this.level = rLevel;
        }

        // 从下往上插入节点
        Node<E> node = new Node<>(item, rLevel);
        for (int i = 0; i <= rLevel; i++) {
            current = stack.pop();
            node.next[i] = current.next[i];
            current.next[i] = node;
        }
    }

  • 跳跃表中删除元素

    删除过程与查询过程类似，只是需要从下往上依次删除待删除元素即可。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    public void delete(E item) {
        // 栈，用于存放各个层级上最后一个小于待删除元素的节点。
        ArrayDeque<Node<E>> stack = new ArrayDeque<>();
        // 当前搜索节点
        Node<E> current = this.head;

        for (int i = this.maxLevel; i >= 0; i--) {
            // 当前层级之下当前节点的下一个节点存在，且值小于或等于待删除元素，则继续向前搜索。
            while (null != current.next[i] && comparator.compare(current.next[i].item, item) < 0) {
                current = current.next[i];
            }
            // 当前节点为当前层级之上最后一个小于或等于待删除元素的节点，故将其添加至栈中。
            stack.push(current);
        }

        Node<E> deleteNode = current.next[0];

        // 如果待删除节点不存在，则直接退出即可。
        if (null == deleteNode || comparator.compare(deleteNode.item, item) != 0) {
            return ;
        }

        int deleteLevel = deleteNode.next.length - 1;

        // 删除待删除节点
        for (int i = 0; i <= deleteLevel; i++) {
            current = stack.pop();
            current.next[i] = deleteNode.next[i];
        }

        // 更新当前跳跃表中最大层级数。
        while (this.level > 0 && null == this.head.next[this.level]) {
            this.level--;
        }
    }

    拓展

不确定性跳跃表

这里探讨两个比较简单的问题：

  1. 跳跃表中节点包含的平均引用数目是多少？

    查看函数 “指定层级数”，我们可以发现节点包含的引用数目满足一个概率分布：

    • 节点包含的引用数目为一的概率为 $(1 - p)$；
    • 节点包含的引用数目为二的概率为 $p(1 - p)$；
    • 节点包含的引用数目为三的概率为 $p^2(1 - p)$；
    • $\dots$

    那么跳跃表中节点包含的平均引用数目可计算如下：

    $1 \times (1 - p) + 2 \times p(1 - p) + 3 \times p^2(1 - p) + \dots = (1 - p)\sum_{i = 1}^{\infty}(i \times p^{i - 1}) = (1 - p) \times \frac{1}{(1 - p)^2} = \frac{1}{1 - p}$

    依据推导结果，我们可以看到：节点包含的平均引用数目与指定的概率参数相关，且指定的概率参数值越小，节点包含的平均引用数目越少。

    当 $p = 1/2$ 时，节点包含的平均引用数目为 $2$；当 $p = 1/4$ 时，节点包含的平均引用数目为 $1.33$。

  2. 与平衡树、哈希表的比较？

    查找性能比较优良的数据结构就这三种：平衡树、哈希表和跳跃表。故而在此简要对比一下三者：

    • 哈希表中元素无序排列，而平衡树与跳跃表中元素有序排列。故而前者只能进行单个查询，后者即可进行单个查询，又可进行范围查询。
    • 进行单个查询时，哈希表可达到 $O(1)$ 的时间复杂度，平衡树和跳跃表的时间复杂度为 $O(log^N)$。
    • 进行范围查询时，平衡树操作较为复杂，原因在于：找到范围起点后，需中序遍历平衡树直至范围终点。而对跳跃表而言，只要在第零层级向前搜索到范围终点即可。
    • 平衡树插入、删除操作可能引发子树调整，故而逻辑复杂。哈希表和跳跃表只需要修改相关节点引用即可，比较简单。
    • 从无关数据的内存占用上来说，平衡树通常需要 $2-3$ 个节点引用 (左右儿子节点、父节点)；跳跃表通过指定概率参数可仅使用 $1.33$ 个节点引用。

确定性跳跃表

此处简要介绍其中一种确定性跳跃表—— 1-2-3 确定性跳跃表。

我们首先做出如下两个定义：

  1. 如果至少存在一个链从一个元素指向另一个元素，我们就称两个元素是 链接的。
  2. 第 $h$ 层级之上的两个链接元素间的 间隙容量 等于第 $h - 1$ 层级中这两个元素间的元素个数。

1-2-3 确定性跳跃表满足如下性质：任意链接元素间的间隙容量只可能是 1 或 2 或 3。

图三即为确定性跳跃表的一个例子。其中第一层级之上的两个链接元素 ( $10$ 与 $25$ ) 间的间隙容量等于第零层级中这两个元素间的元素个数 ( $15$ 与 $20$，共计两个元素 )。
图三：确定性跳跃表

接下来我们介绍一下确定性跳跃表中的插入与删除操作：

  • 插入操作

    插入操作可能使得某链接元素间的间隙容量扩大为 $4$，故而需要进行适当拆分。

    一种可行的做法为：向下搜索插入位置之时，如果当前节点与后继节点间的间隙容量为 $3$，则令下一层级中位于中间的那个节点的层级加一，使得其成为当前节点的后继节点。

    图四所示为向跳跃表中插入元素 $27$ 。由于第二层级之上首尾两个元素间的间隙容量为 $3$，故而提升下一层级中的 $25$，使得其与首节点的间隙容量、其与尾节点的间隙容量均为 $1$，此时在这两者间插入元素则不再会破坏性质。

    图四：插入元素27

  • 删除操作

    删除操作可能使得某链接元素间的间隙容量缩小为 $0$，故而需要进行适当合并。

    一种可行的做法为：向下搜索删除元素过程中，如果当前节点与后继节点间的间隙容量为 $1$，那么删除指定元素后，可能会破坏此处的性质，因此我们需要扩大当前节点与后继节点间的间隙容量。如果后继节点与后继节点的后继节点的间隙容量大于 $1$，我们便从后继节点借 $1$ 个间隙容量；如果后继节点与后继节点的后继节点的间隙容量等于 $1$，我们便降低后继节点的层级，此时当前节点与新后继节点的间隙容量就为 $3$。

图中所示仅为确定性跳跃表的表示图，其逻辑结构与此还是有一定区别的。

相关文章