数据结构-Treap树/替罪羊树

发表于 分类于
本文字数： 3.6k 阅读时长 ≈ 3 分钟

概述

Treap 树 是一个附加域满足堆性质的二叉查找树，其基本操作的期望时间复杂度为 $O(log^N)$。相比于 AVL、红黑树而言，其实现简单，且能基本实现随机平衡。

其结构图大致如下：

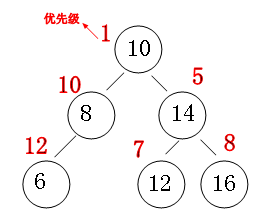
图一：Treap树

对于二叉查找树而言，特殊插入序列将会使得二叉查找树退化为一个链表，这样会大大降低二叉查找树的性能。为避免这一情况的发生，AVL 限制左右子树高度差不超过 1、红黑树要求任意节点到其所有后代叶节点的简单路径均包含相同数目的黑色节点。对于 Treap 树而言，要求附加域满足堆性质使得不存在特殊插入序列，从而避免这一情况的发生 (查看下面的插入过程就可理解这句话)。

结构

附加域即是该节点的优先级，它在建立节点时随机指定。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Treap<E> {
    // 节点结构
    private static class Node<E> {
        // 具体元素
        E item;
        // 左儿子
        Node<E> left;
        // 右儿子
        Node<E> right;
        // 优先级
        int priority;

        public Node(E item, int priority) {
            this.item = item;
            this.left = null;
            this.right = null;
            this.priority = priority;
        }
    }
    // 比较函数
    private final Comparator<? super E> comparator;
    // 根节点
    private Node<E> root;
    // 随机函数
    private static Random random = new Random(System.currentTimeMillis());
}

实现

辅助方法

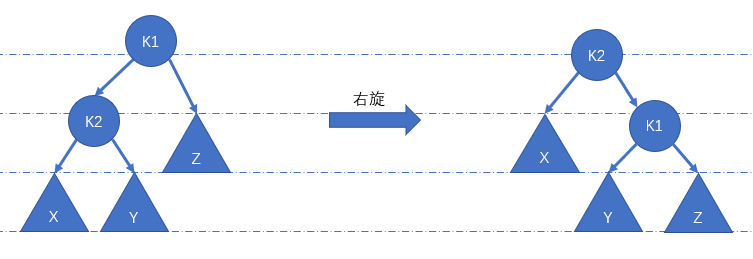
  • 右旋

    Treap 树中两大基本操作之一，用于维持堆性质。

    图二：右旋

    1
    2
    3
    4
    5
    6
    7
    8
    private Node<E> rightRotate(Node<E> root) {
        Node<E> k1 = root;
        Node<E> k2 = root.left;

        k1.left = k2.right;
        k2.right = k1;
        return k2;
    }

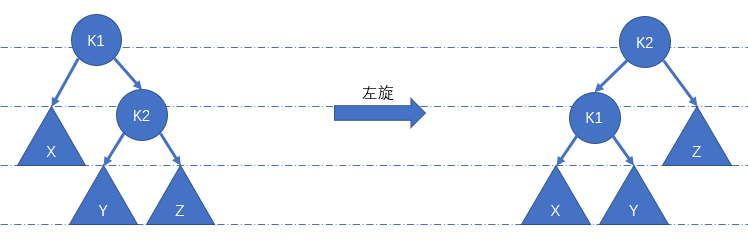
  • 左旋

    Treap 树中两大基本操作之一，用于维持堆性质。

    图三：左旋

    1
    2
    3
    4
    5
    6
    7
    8
    private Node<E> leftRotate(Node<E> root) {
        Node<E> k1 = root;
        Node<E> k2 = root.right;

        k1.right = k2.left;
        k2.left = k1;
        return k2;
    }

  • 当前子树中插入元素，并返回插入元素后的该子树

    插入过程与二叉查找树插入过程基本相同，不同点即在于：将元素插入到合适位置之后，如果堆性质不满足，需借助于左旋或右旋进行调整。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    private Node<E> addTree(E item, Node<E> root) {
        // 当前子树为空，创建该节点并返回即可。
        if (null == root) {
            return new Node<>(item, random.nextInt());
        }

        // 当前子树根节点值大于指定元素，则应当插入于左子树之中。
        if (comparator.compare(root.item, item) > 0) {
            root.left = addTree(item, root.left);

            // 如果子节点优先级低于当前节点优先级，则需进行右旋。
            if (root.left.priority < root.priority) {
                root = rightRotate(root);
            }
        } else if (comparator.compare(root.item, item) < 0) {
            // 当前子树根节点值小于指定元素，则应当插入于右子树之中。
            root.right = addTree(item, root.right);

            // 如果子节点优先级低于当前节点优先级，则需进行左旋。
            if (root.right.priority < root.priority) {
                root = leftRotate(root);
            }
        }

        return root;
    }

  • 当前子树中删除元素，并返回删除元素后的该子树

    删除元素过程比较巧妙。借助于左旋与右旋，逐步将待删除节点下沉至叶节点，然后直接删除即可。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    private Node<E> deleteTree(E item, Node<E> root) {
        // 当前子树为空，直接返回空即可。
        if (null == root) {
            return null;
        }

        // 当前子树根节点值大于待删除元素，则待删除元素一定位于左子树之中。
        if (comparator.compare(root.item, item) > 0) {
            root.left = deleteTree(item, root.left);
        } else if (comparator.compare(root.item, item) < 0) {
            // 当前子树根节点值小于待删除元素，则待删除元素一定位于右子树之中。
            root.right = deleteTree(item, root.right);
        } else {
            // 当前子树根节点值等于待删除元素，此即为待删除元素。
            // 只要左右儿子一者为空，则直接使用另一儿子节点所在子树代替当前子树即可。
            if (null == root.right) {
                root = root.left;
            } else if (null == root.left) {
                root = root.right;
            } else {
                // 当前子树根节点的左右儿子均不为空。
                // 借助左旋或右旋使待删除节点下沉至叶节点，然后删除即可。
                if (root.left.priority < root.right.priority) {
                    root = rightRotate(root);
                    root.right = deleteTree(item, root.right);
                } else {
                    root = leftRotate(root);
                    root.left = deleteTree(item, root.left);
                }
            }
        }

        return root;
    }

    初始化

1
2
3
public Treap(Comparator<? super E> comparator) {
    this.comparator = comparator;
}

操纵

  • Treap 树中添加元素

    1
    2
    3
    public void add(E item) {
        this.root = addTree(item, this.root);
    }

  • Treap 树中删除元素

    1
    2
    3
    public void delete(E item) {
        this.root = deleteTree(item, this.root);
    }

    扩展

替罪羊树

替罪羊树 是一种非常优雅的二叉查找树。如果当前子树极度不平衡，替罪羊树首先将中序遍历该子树的结果置于数组之中，然后按照 “以中间值元素为根节点，左半部分元素构建左子树，右半部分元素构建右子树” 的方式重构该子树。

接下来我们谈谈替罪羊树上的一些操作：

  • 插入操作

    与普通二叉查找树的插入操作基本相同，不同点在于：插入完成后，递归向上至根节点过程中，找到最后一棵极度不平衡的子树，然后重构它。由于此过程并不常发生，所以其平均时间复杂度为 $O(log^N)$ 。

  • 删除操作

    删除过程采用 “懒惰删除”，即并不立即删除该节点，只是标记该节点为已删除节点。如果当前子树中已删除节点个数/当前子树中所有节点个数大于某一阈值，则在重构过程中删除这些节点。理论已经证明，其平均时间复杂度仍为 $O(log^N)$ 。

  • 查询操作

    与普通二叉查找树的查询操作基本相同，不同点在于：如果当前节点为已删除节点，直接忽略它即可。故而其平均时间复杂度为 $O(log^N)$ 。

“当前子树极度不平衡” 的衡量条件为：$$size(root.left) / size(root) > \alpha \ || \ size(root.right) / size(root) > \alpha$$，其中 $size(x)$ 表示以当前节点为根节点的子树中节点数量、$\alpha$ 为衡量阈值。

相关文章