数据结构-红黑树
概述
红黑树 是一种自平衡的二叉查找树。通过为树中节点添加颜色属性并施以一定规则,红黑树可保证针对二叉查找树各种操作的最坏时间复杂度为 $O(log^N)$。
其结构图大致如下:
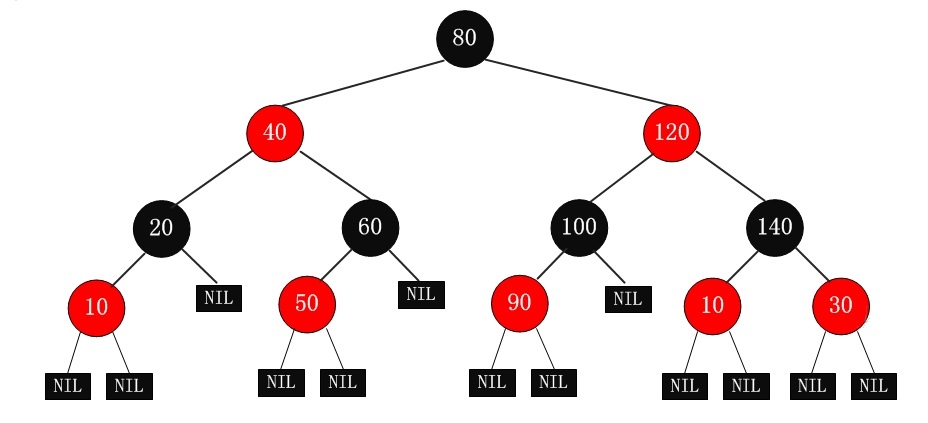
一棵红黑树是满足如下 红黑性质 的二叉查找树:
- 每个节点的颜色属性要么是红色,要么是黑色。
- 根节点的颜色属性为黑色。
- 每个叶节点 (
NIL) 的颜色属性为黑色。 - 如果一个节点的颜色属性为红色,则其孩子节点的颜色属性一定为黑色。
- 对于每个节点而言,从该节点到其所有后代叶节点的简单路径中,均包含相同数目的黑色节点。
基于上述红黑性质,我们可以得到如下结论:一棵含有 $N$ 个内部节点的红黑树,其高度至多为 $O(2log^{N + 1})$。正是此结论,保证了针对二叉查找树各种操作的最坏时间复杂度为 $O(log^N)$。
结构
红黑树需额外保存节点的颜色信息。
1 | class RBTree<E> { |
实现
辅助方法
当前节点颜色是否为黑色
1
2
3private boolean isBlack(Node<E> node) {
return (null == node) || (node.isBlack);
}当前节点颜色是否为红色
1
2
3private boolean isRed(Node<E> node) {
return !isBlack(node);
}当前子树中查找具有最小元素的节点
1
2
3
4
5
6
7
8
9
10
11
12private Node<E> getMinTree(Node<E> root) {
if (null == root) {
return null;
}
// 一路向左即可。
Node<E> node = root;
while (null != node.left) {
node = node.left;
}
return node;
}右旋
该操作就是 AVL 中的
LL,也是伸展树中的zig。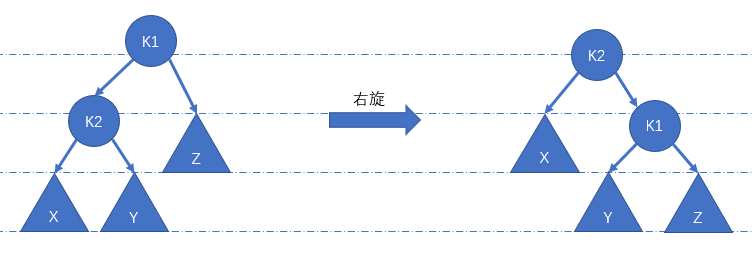
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27private void rightRotate(Node<E> root) {
Node<E> k1 = root;
Node<E> k2 = root.left;
// 首先调整k1左儿子指向及相应儿子的父节点指向。
k1.left = k2.right;
if (null != k2.right) {
k2.right.parent = k1;
}
// 其次调整k2的父节点指向及相应父节点的儿子节点指向。
// 如果k2.parent为空,表明k2为根结点,需重新指定根结点。
k2.parent = k1.parent;
if (null != k1.parent) {
if (k1 == k1.parent.left) {
k1.parent.left = k2;
} else {
k1.parent.right = k2;
}
} else {
this.root = k2;
}
// 最后调整k1的右儿子指向及相应儿子的父节点指向。
k2.right = k1;
k1.parent = k2;
}左旋
该操作就是 AVL 中的
RR,也是伸展树中的zag。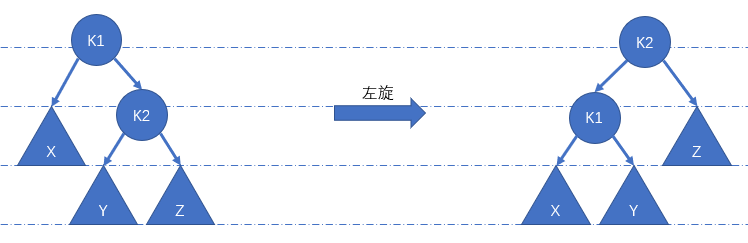
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27private void leftRotate(Node<E> root) {
Node<E> k1 = root;
Node<E> k2 = root.right;
// 首先调整k1右儿子指向及相应儿子的父节点指向。
k1.right = k2.left;
if (null != k2.left) {
k2.left.parent = k1;
}
// 其次调整k2的父节点指向及相应父节点的儿子指向。
// 如果k1.parent为空,表明k1为根结点,需重新指定根结点。
k2.parent = k1.parent;
if (null != k1.parent) {
if (k1 == k1.parent.left) {
k1.parent.left = k2;
} else {
k1.parent.right = k2;
}
} else {
this.root = k2;
}
// 最后调整k2右儿子及相应儿子的父节点指向。
k2.left = k1;
k1.parent = k2;
}插入修正
向红黑树中插入元素时,可能会破坏红黑性质,因此需要对红黑树进行一定调整。
当向红黑树中插入元素时,我们需要指定新建节点的颜色。如果指定为黑色,红黑性质五一定遭到破坏,故而需要进行调整;如果指定为红色,只有当其父节点的颜色同样为红色时,红黑性质四才会遭到破坏,此时需要进行调整。考虑到编码简洁性,我们指定新建节点的颜色为红色。
插入修正涉及多种情景,我们在此一一详述 (假定此时新建节点已插入到合适位置。图例中
C表示当前节点,P表示父节点,PP表示祖父节点,U表示叔叔节点。)。插入情景1:红黑树为空
将当前节点指定为根节点,并将节点颜色置为黑色。
插入情景2:当前节点的父节点颜色为黑色
无需做任何处理。
插入情景3:当前节点的父节点颜色为红色
当前节点颜色与父节点颜色同为红色,违反红黑性质四,故而需要进行调整。由于父节点颜色为红色,根据红黑性质四可知祖父节点一定存在。考虑到祖父节点及叔叔节点颜色的不确定性,此情景又可进一步细分为如下子情景。
插入情景3.1: 当前节点的父节点为祖父节点的左儿子
插入情景3.1.1:叔叔节点存在且颜色为红色
为维持红黑性质,我们只需要将
P和U置为黑色、PP置为红色,同时重置节点PP为当前节点,递归处理当前节点即可。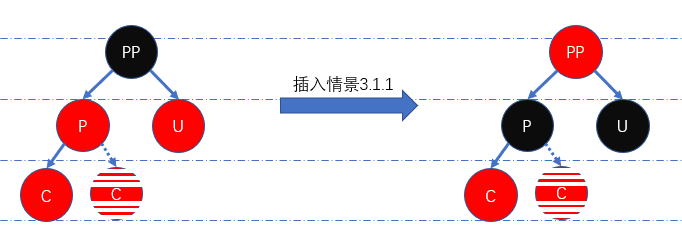
插入情景3.1.2:叔叔节点不存在或存在且颜色为黑色,并且当前节点为父节点的左儿子
这里有关叔叔节点的表述存在一定问题。由于祖父节点满足红黑性质,那么容易得知叔叔节点一定是空节点。此时为维持红黑性质,我们需要先将
P置为黑色、PP置为红色,然后右旋节点PP即可。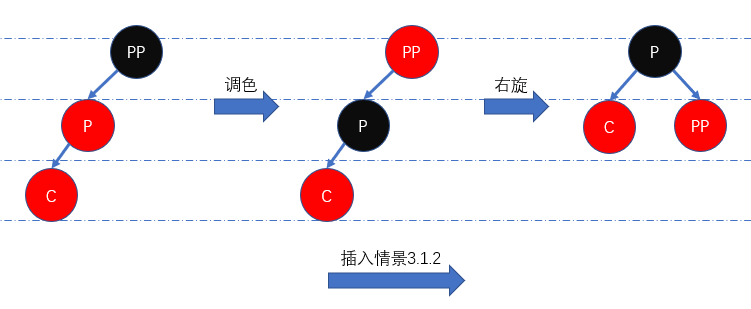
插入情景3.1.3: 叔叔节点不存在或存在且颜色为黑色,并且当前节点为父节点的右儿子
这里有关叔叔节点的表述存在一定问题。由于祖父节点满足红黑性质,那么容易得知叔叔节点一定是空节点。此时为维持红黑性质,我们先左旋节点
P,然后重置节点P为当前节点,最后使用 插入情景3.1.2 的处理方法即可。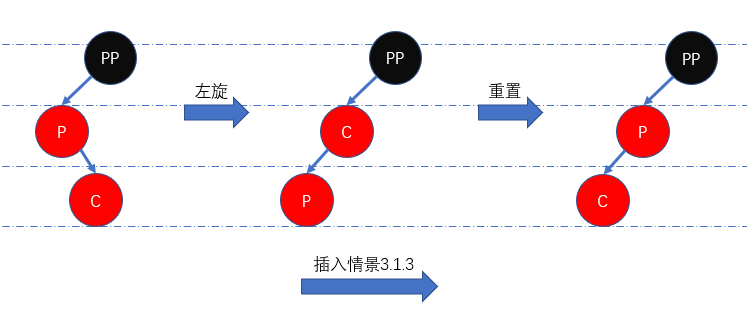
插入情景3.2: 当前节点的父节点为祖父节点的右儿子
插入情景3.2.1: 叔叔节点存在且颜色为红色
为维持红黑性质,我们只需要将
P和U置为黑色、PP置为红色,同时重置节点PP为当前节点,递归处理 当前节点即可。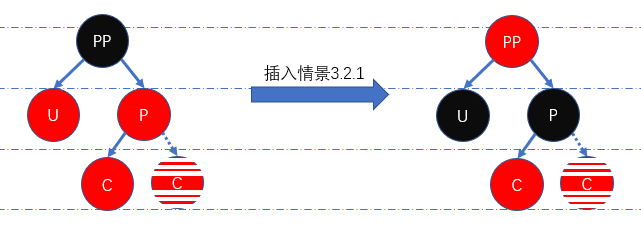
插入情景3.2.2: 叔叔节点不存在或存在且颜色为黑色,并且当前节点为父节点的右儿子
这里有关叔叔节点的表述存在一定问题。由于祖父节点满足红黑性质,那么容易得知叔叔节点一定是空节点。此时为维持红黑性质,我们需要先将
P置为黑色、PP置为红色,然后左旋节点PP即可。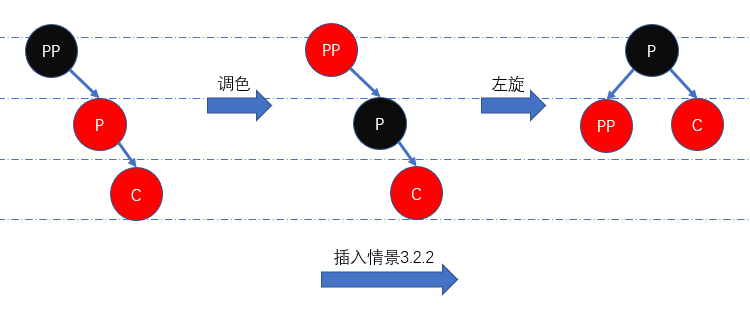
插入情景3.2.3: 叔叔节点不存在或存在且颜色为黑色,并且当前节点为父节点的左儿子
这里有关叔叔节点的表述存在一定问题。由于祖父节点满足红黑性质,那么容易得知叔叔节点一定是空节点。此时为维持红黑性质,我们先右旋节点
P,然后重置节点P为当前节点,最后使用 插入情景3.2.2 的处理方法即可。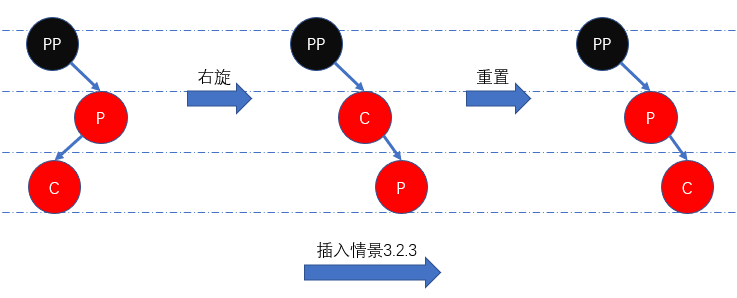
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65// 插入情景1,2已在它处加以处理,此函数仅处理插入情景3。
private void insertFixUp(Node<E> root) {
// 如果当前节点的父节点存在,且节点颜色为红色,则需要调整。
while (null != root.parent && isRed(root.parent)) {
// 获取父节点和祖父节点引用。
Node<E> parent = root.parent;
Node<E> grandParent = parent.parent;
// 父节点为祖父节点的左儿子。
if (parent == grandParent.left) {
Node<E> uncle = grandParent.right;
// 插入情景3.1.1:叔叔节点存在且颜色为红色。
if (null != uncle && isRed(uncle)) {
parent.setBlack();
uncle.setBlack();
grandParent.setRed();
root = grandParent;
continue;
}
// 插入情景3.1.3:叔叔节点不存在或存在且颜色为黑色,并且当前节点为父节点的右儿子。
if (root == parent.right) {
leftRotate(parent);
Node<E> tmp;
tmp = root;
root = parent;
parent = tmp;
}
// 插入情景3.1.2:叔叔节点不存在或存在且颜色为黑色,并且当前节点为父节点的左儿子。
rightRotate(grandParent);
parent.setBlack();
grandParent.setRed();
} else {
// 父节点为祖父节点的右儿子。
Node<E> uncle = grandParent.left;
// 插入情景3.2.1: 叔叔节点存在且颜色为红色。
if (null != uncle && isRed(uncle)) {
parent.setBlack();
uncle.setBlack();
grandParent.setRed();
root = grandParent;
continue;
}
// 插入情景3.2.3: 叔叔节点不存在或存在且颜色为黑色,并且当前节点为父节点的左儿子。
if (root == parent.left) {
rightRotate(parent);
Node<E> tmp;
tmp = root;
root = parent;
parent = tmp;
}
// 插入情景3.2.2: 叔叔节点不存在或存在且颜色为黑色,并且当前节点为父节点的右儿子。
leftRotate(grandParent);
parent.setBlack();
grandParent.setRed();
}
}
// 上述调整可能导致根结点变为红色,在此需要调整。
this.root.setBlack();
}删除子过程
将前者节点所在子树替换为后者节点所在子树,同时调整前者节点父节点的孩子节点指向。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15private void judgeParent(Node<E> former, Node<E> latter) {
latter.parent = former.parent;
// 前者的父节点为空,表明其为根节点,故而需要调整root指向。
if (null == former.parent) {
this.root = latter;
}
// 调整前者父节点的孩子指向。
if (former == former.parent.left) {
former.parent.left = latter;
} else {
former.parent.right = latter;
}
}删除修正
如果待删除节点颜色为黑色,红黑性质五则会遭到破坏,此时需要对红黑树进行一定调整。
删除修正涉及多种情景,我们在此一一详述 (假定此时待删除节点已删除完成,我们需要对顶替待删除节点所在位置的那个节点进行调整操作。图例中
C表示当前节点,即顶替待删除节点所在位置的那个节点,P表示父节点,B表示兄弟节点,LB表示兄弟节点的左儿子,RB表示兄弟节点的右儿子,节点颜色为灰色表示该节点颜色或为红色、或为黑色。)。- 为保证删除节点后的红黑树满足红黑性质,我们暂且视当前节点额外具有一重黑色。故而下面图例中,我们直接将当前节点颜色置为黑色。
- 如果待删除节点颜色为黑色,那么根据红黑性质五容易得知:兄弟节点一定存在。
删除情景1: 当前节点为父节点的左儿子
删除情景1.1: 兄弟节点颜色为红色
当兄弟节点颜色为红色时,根据红黑性质可容易推知其他相关节点颜色。为维持红黑性质,我们需要先将
P置为红色、B置为黑色,然后左旋节点P,最后使用 删除情景1.2 的处理方法即可。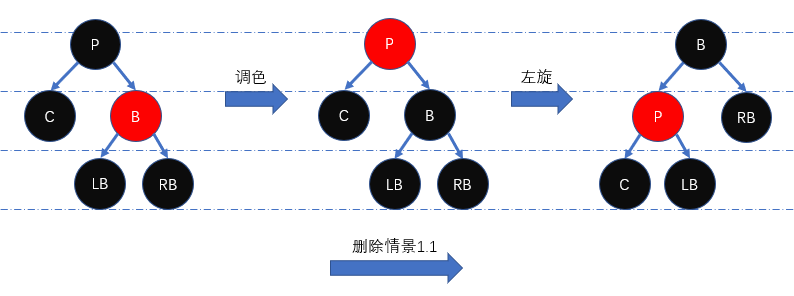
删除情景1.2: 兄弟节点颜色为黑色
删除情景1.2.1: 兄弟节点的左右儿子节点颜色均为黑色
为维持红黑性质,我们需先将
B置为红色,C恢复为原本颜色,然后重置节点P为当前节点,最后递归处理当前节点即可。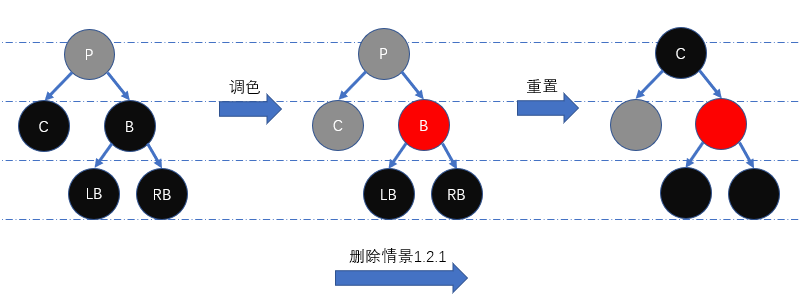
删除情景1.2.2: 兄弟节点的左儿子颜色为红色,右儿子颜色为黑色
为维持红黑性质,我们需先将
LB置为黑色、B置为红色,然后右旋节点B,最后使用 删除情景1.2.3 的处理方法即可。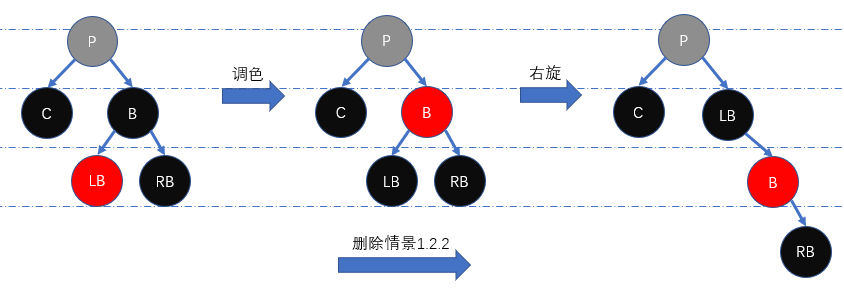
删除情景1.2.3: 兄弟节点的左儿子颜色任意,右儿子颜色为红色
为维持红黑性质,我们需先将
B置节点P原本的颜色、P置为黑色、RB置为黑色、C恢复为原本颜色,然后左旋节点P即可。此情景为删除修正中最为重要的情景,我们在此说明一下 “为什么如下转换是可行的? “。
通过为当前节点添加一重额外的黑色,未调整前的红黑树是满足红黑性质的,此时我们可得到如下等式:$hb(C) = hb(LB) + 1;hb(RB) = hb(LB)$。 通过一系列颜色调整,使得
C所在子树的黑高减一、RB所在子树的黑高加一,最终可得到如下等式:$hb(C) = hb(LB);hb(RB) = hb(LB) + 1$。此时对于P和B而言,红黑性质五均得到满足,调整完成。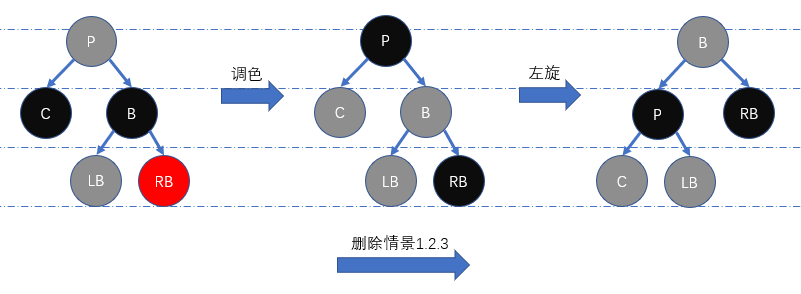
删除情景2: 当前节点为父节点的右儿子
删除情景2.1: 兄弟节点颜色为红色
当兄弟节点颜色为红色时,根据红黑性质可容易推知其他相关节点颜色。为维持红黑性质,我们需要先将
P置为红色、B置为黑色,然后右旋节点P,最后使用 删除情景2.2 的处理方法即可。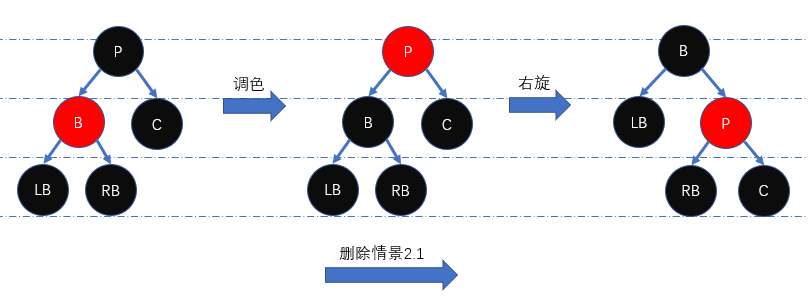
删除情景2.2: 兄弟节点颜色为黑色
删除情景2.2.1: 兄弟节点的左右儿子节点颜色均为黑色
为维持红黑性质,我们需先将
B置为红色,C恢复为原本颜色,然后重置节点P为当前节点,最后递归处理当前节点即可。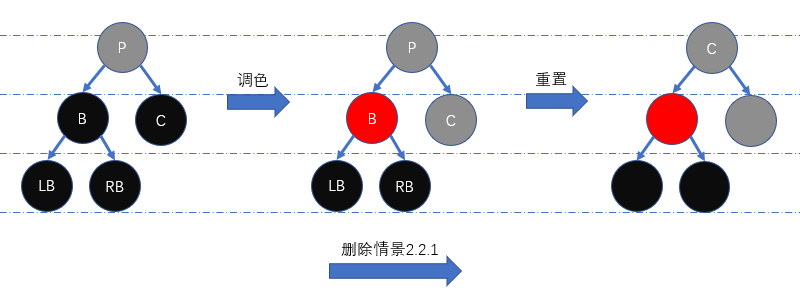
删除情景2.2.2: 兄弟节点的左儿子颜色为黑色,右儿子颜色为红色
为维持红黑性质,我们需先将
RB置为黑色、B置为红色,然后左旋节点B,最后使用 删除情景2.2.3 的处理方法即可。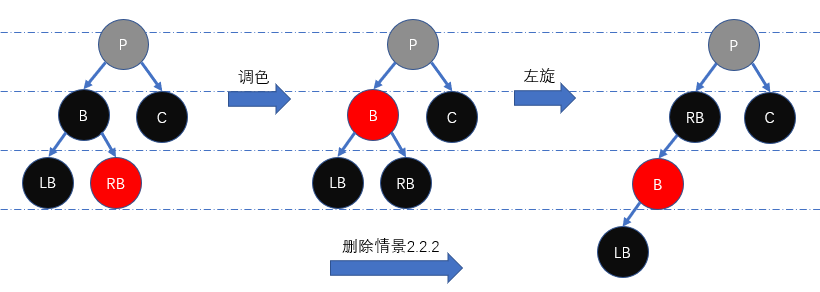
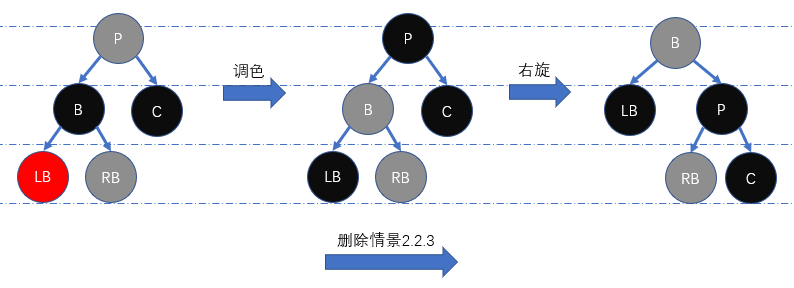
删除情景2.2.3: 兄弟节点的左儿子为红色,右儿子颜色为任意颜色
为维持红黑性质,我们需先将
B置节点P原本的颜色、P置为黑色、LB置为黑色、C恢复为原本颜色,然后右旋节点P即可。转换可行性解释与 删除情景1.2.3 类似。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83private void deleteFixUp(Node<E> root, Node<E> parent) {
// 调整结束条件:root不为红黑树根节点。
while (root != this.root) {
// root节点为父节点左儿子。
if (root == parent.left) {
// 获取root节点的兄弟节点。
Node<E> brother = parent.right;
// 删除情景1.1:兄弟节点颜色为红色。
if (isRed(brother)) {
leftRotate(parent);
parent.setRed();
brother.setBlack();
// 更新root节点的兄弟节点。
brother = parent.right;
}
// 删除情景1.2.1:兄弟节点的左右儿子节点颜色均为黑色。
if (isBlack(brother.left) && isBlack(brother.right)) {
brother.setRed();
root = parent;
// 更新root节点的父节点。
parent = root.parent;
} else if (isBlack(brother.right)) {
// 删除情景1.2.2:兄弟节点的左儿子颜色为红色,右儿子颜色为黑色。
rightRotate(brother);
brother.left.setBlack();
brother.setRed();
// 更新root节点的兄弟节点。
brother = parent.right;
} else {
// 删除情景1.2.3:兄弟节点的左儿子颜色任意,右儿子颜色为红色。
brother.isBlack = parent.isBlack;
parent.setBlack();
brother.right.setBlack();
leftRotate(parent);
// 此一调整可保证红黑树性质得以满足,直接退出即可。
break;
}
} else {
// root节点为父节点右儿子。
Node<E> brother = parent.left;
// 删除情景2.1:兄弟节点颜色为红色。
if (isRed(brother)) {
rightRotate(parent);
parent.setRed();
brother.setBlack();
// 更新root节点的兄弟节点。
brother = parent.left;
}
// 删除情景2.2.1:兄弟节点的左右儿子节点颜色均为黑色。
if (isBlack(brother.left) && isBlack(brother.right)) {
brother.setRed();
root = parent;
// 更新root节点的父节点。
parent = root.parent;
} else if (isBlack(brother.left)) {
// 删除情景2.2.2:兄弟节点的左儿子颜色为黑色,右儿子颜色为红色。
leftRotate(brother);
brother.right.setBlack();
brother.setRed();
// 更新root节点的兄弟节点。
brother = parent.left;
} else {
// 删除情景2.2.3:兄弟节点的左儿子为红色,右儿子颜色为任意颜色。
brother.isBlack = parent.isBlack;
parent.setBlack();
brother.left.setBlack();
rightRotate(parent);
// 此一调整可保证红黑树性质得以满足,直接退出即可。
break;
}
}
}
if (null != this.root) {
this.root.setBlack();
}
}该函数需要注意一点:传参时需要传入待调整节点的父节点。其原因在于:待调整节点可能为空节点,空节点是无法直接找到其父节点的。
初始化
1 | public RBTree(Comparator<? super E> comparator) { |
操纵
红黑树中添加元素
添加元素过程与二叉查找树基本相同,只是在最后多了一个 “插入修正”。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40public void add(E item) {
// 红黑树为空,直接创建该节点即可。
if (null == this.root) {
this.root = new Node<>(item);
this.root.isBlack = true;
return;
}
// 指向插入节点。
Node<E> node = this.root;
while (true) {
// 当前节点元素值大于待插入值,则应插入于左子树。
if (comparator.compare(node.item, item) > 0) {
if (null == node.left) {
node.left = new Node<>(item);
node.left.parent = node;
node = node.left;
break;
} else {
node = node.left;
}
} else if (comparator.compare(node.item, item) == 0) {
// 当前节点元素值等于待插入值,直接返回即可。
return;
} else {
// 当前节点元素值小于待插入值,则应插入于右子树。
if (null == node.right) {
node.right = new Node<>(item);
node.right.parent = node;
node = node.right;
break;
} else {
node = node.right;
}
}
}
// 插入修正。
insertFixUp(node);
}红黑树中删除元素
删除元素过程同样与二叉查找树类似,只是额外多了两个步骤:记录待删除节点颜色以及 “删除修正”。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75public void delete(E item) {
// 指向待删除节点。
Node<E> node = this.root;
// 指向待调整节点。
Node<E> judgeNode = null;
// 指向待调整节点的父节点。
Node<E> judgeNodeParent = null;
// 待删除节点是否为黑色。
boolean isBlack = false;
while (null != node) {
if (comparator.compare(node.item, item) > 0) {
node = node.left;
} else if (comparator.compare(node.item, item) == 0) {
break;
} else {
node = node.right;
}
}
// 红黑树为空或者不存在具有该元素的节点,直接返回即可。
if (null == node) {
return;
}
isBlack = node.isBlack;
// 待删除节点的左右子树均不为空。
if (null != node.left && null != node.right) {
// 获取后继节点。
Node<E> next = getMinTree(root.right);
// 将待删除节点调整为后继节点。
// 这里有多种方式可以采取。例如直接交换关键字、直接交换这两个节点所有引用指向。
// 直接交换二者关键字
E tmp;
tmp = next.item;
next.item = node.item;
node.item = tmp;
// 更新node指向及isBlack取值。
node = next;
isBlack = node.isBlack;
}
// 待删除节点左子树不为空。
if (null != node.left) {
judgeNode = node.left;
judgeParent(node, judgeNode);
judgeNodeParent = judgeNode.parent;
} else if (null != node.right) {
// 待删除节点右子树为空。
judgeNode = node.right;
judgeParent(node, judgeNode);
judgeNodeParent = judgeNode.parent;
} else {
// 左右子树均为空。
judgeNodeParent = node.parent;
if (null == node.parent) {
this.root = null;
} else {
if (node == node.parent.left) {
node.parent.left = null;
} else {
node.parent.right = null;
}
}
}
// 删除节点为黑节点,则需要进行调整。
if (isBlack) {
deleteFixUp(judgeNode, judgeNodeParent);
}
}扩展
自顶向下红黑树
上面所示代码为自底向上实现红黑树,另外还可自顶向下实现红黑树,此种做法的优点在于无需存储父节点信息。
红黑树中添加元素
自底向上实现红黑树中,当叔叔节点颜色为红色时,需要向上递归处理;当叔叔节点颜色为黑色时,只需要处理当前节点、父节点和祖父节点。因此,为自顶向下实现红黑树,只需要使用一定规则保证 “当需要进行调整时叔叔节点颜色不可能为红色” 即可。
这一规则具体内容如图示:
如果当前节点的左右儿子节点颜色均为红色,那么便置当前节点颜色为红色,左右儿子节点颜色为黑色。
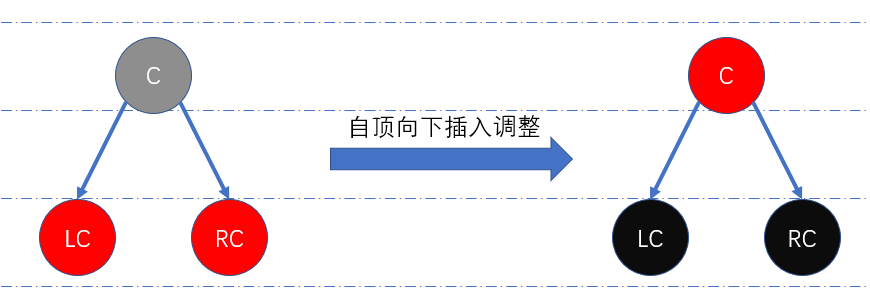
自顶向下实现红黑树中添加元素具体步骤如下:
- 初始化当前节点为
this.root、父节点为null、祖父节点为null。 - 如果当前节点左右儿子节点颜色均为红色,则采用上图加以调整。
- 如果当前节点父节点颜色亦为红色,则根据当前节点、父节点、祖父节点间关系进行调整。
- 如果当前节点父节点颜色为黑色,则直接跳转到 步骤 6 。
- 将当前节点元素值与待插入元素值进行对比,更新当前节点、父节点、祖父节点,跳转到 步骤 2。
- 设置根节点颜色为黑色。
- 初始化当前节点为
红黑树中删除元素
自底向上实现红黑树中,我们将删除元素转换为 “删除一个至少含有一个空儿子节点的节点”。当待删除节点的一个儿子节点为空、另一个儿子节点不为空时,我们还可取不空儿子节点所在子树中的最大值/最小值所在节点替换待删除节点,并指定该节点成为待删除节点。依此思路而行,最终待删除节点的左右儿子节点均为空节点。故而,我们便将删除元素进一步转换为 “删除一个两个儿子节点均为空节点的节点”。
如果待删除节点颜色为红色,那么直接删除即可;反之删除后需调整红黑性质。为自顶向下实现红黑树,只需要使用一定规则保证 “当前正在处理的节点颜色为红色” 即可。
假定某一轮调整已保证当前正在处理的节点颜色为红色,如果当前节点并非待删除节点,那么我们需要进一步向下探索,如此可得到如图情况:
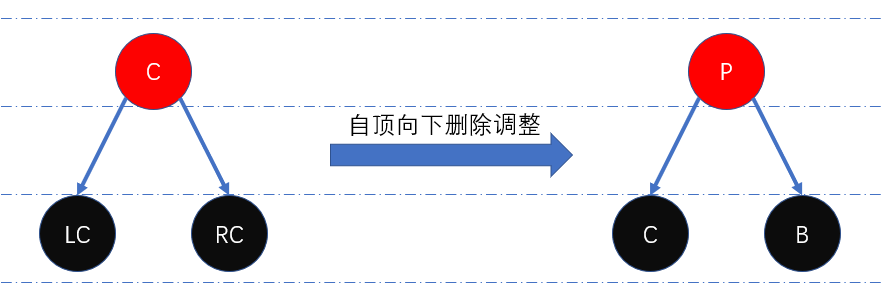
此时我们便需要使用一定规则将当前节点颜色调整为红色,这样便可进一步向下探索。最终我们将得到:待删除节点的左右儿子为空,且待删除节点颜色为红色,此时直接删除该节点即可。
这里涉及的规则比较复杂,就不说了。
优化红黑树
插入、删除情景众多,使得红黑树实现代码非常复杂。通过对红黑树结构进一步施加限制,可以得到实现较为简单的简化版红黑树,这其中比较著名的有 BB树、AA树。在此我们仅简要介绍 AA 树。
AA 树对红黑树施以如下限制:一个节点最多只有一个红色儿子节点,且该红色儿子节点只能是该节点的右儿子节点。
如此限制结构,使得插入、删除情景各缩减为两种,大大降低了编程复杂性,具体调整就不在叙述了。
扩张红黑树
“扩张红黑树” 指代改造红黑树节点结构以支持特定操作,同时保证红黑树原有各种操作可正常实现。这里介绍两种基于此而实现的数据结构——顺序统计树和区间树。
顺序统计树
顺序统计树可在 $O(log^N)$ 时间内确定指定元素在整棵树中的排名、整棵树中指定排名对应的元素。
向红黑树节点结构中添加字段
size(其意义为:当前节点所在子树含有的节点个数),即可得到顺序统计树的节点结构。实现二叉查找树之时,我顺带实现了顺序统计树,其实现代码参见 数据结构-二叉查找树。
区间树
区间树是一种以区间为元素的数据结构,可在 $O(log^N)$ 时间内实现插入区间元素、删除区间元素、查询与指定区间重叠的区间元素等操作。
区间树的节点结构与红黑树节点结构有较大差别,故而在此列举其结构:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16private static class Node<E> {
// 区间左端点(关键字)
int low;
// 区间右端点
int high;
// 当前子树中所有区间右端点的最大值
int max;
// 父节点
Node<E> parent;
// 左儿子
Node<E> left;
// 右儿子
Node<E> right;
// 节点颜色
boolean isBlack;
}我们使用区间左端点作为关键字参与排序,故而遍历区间树将得到:各区间按左端点的排列次序依次输出。
插入区间元素与删除区间元素的操作与红黑树类似,故而不再叙述。我们在此详述 “查询与指定区间重叠的区间元素” 这一操作。
任意两个区间 $i$ 与 $i’$ 一定满足 区间三分律,即下面三条性质之一成立:
- $i$ 与 $i’$ 重叠 ( $i.low \leq i’.high \ 且 \ i’.low \leq i.high$ )
- $i$ 在 $i’$ 的左边 ( $i.high < i’.low$ )
- $i$ 在 $i’$ 的右边 ( $i.low > i’.high$ )
根据上面这个定理,可容易得到该操作的伪代码:
1
2
3
4
5
6
7
8
9intervalSearch(T, i)
x = T.root;
while (null != x && i does not overlop x)
// x.left.max >= i.low 表明左子树与i重叠,则在该子树中一定可以找到一个区间与i重叠。
if (null != x.left && x.left.max >= i.low)
x = x.left;
else
x = x.right;
return;该伪代码仅查询一个重叠区间元素,其时间复杂度为 $O(log^N)$ 。查找全部重叠区间元素也是可以的,但是时间复杂度就无法保证了。