数据结构-伸展树

发表于 分类于
本文字数： 6.2k 阅读时长 ≈ 6 分钟

概述

伸展树 是一种自调整的二叉查找树。它没有 AVL 那样严格的平衡条件，通过施以某些调整可使得树上各种操作的平均时间复杂度为 $O(log^N)$。

其结构图大致如下：

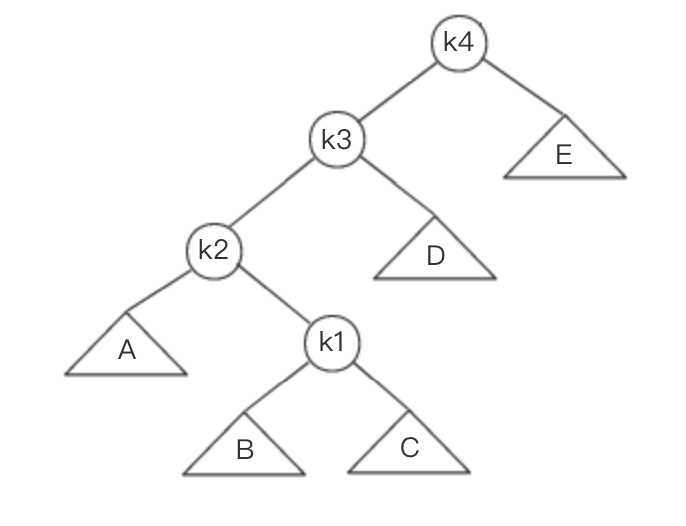
图一：伸展树

我们知道：对于二叉查找树而言，每次操作最坏时间复杂度 $O(N)$ 并非不好，只要它相对不常发生就行。另外我们发现，如果某个节点被访问，那么不久后该节点将再次被访问。基于上述两个事实，伸展树在访问一个节点后，会将该节点旋转至根节点，这样做有两大目的：1. 一定程度上平衡整棵树。2. 降低再次访问该节点所需的时间。

结构

伸展树无需保存高度信息。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class SplayTree<E> {
    // 节点结构
    private static class Node<E> {
        // 具体元素
        E item;
        // 父节点
        Node<E> parent;
        // 左儿子
        Node<E> left;
        // 右儿子
        Node<E> right;

        public Node(E item) {
            this.item = item;
            this.parent = null;
            this.left = null;
            this.right = null;
        }
    }
    // 根节点
    private Node<E> root;
    // 比较函数
    private final Comparator<? super E> comparator;
}

实现

辅助方法

伸展树中的伸展操作主要涉及六大调整，依次为 zig、zag、zig-zig、zag-zag、zig-zag、zag-zig。

  • zig

    通过 zig 调整使节点 K1 成为根节点。

    zig 调整与 AVL 中的 LL 基本相同，同为右旋。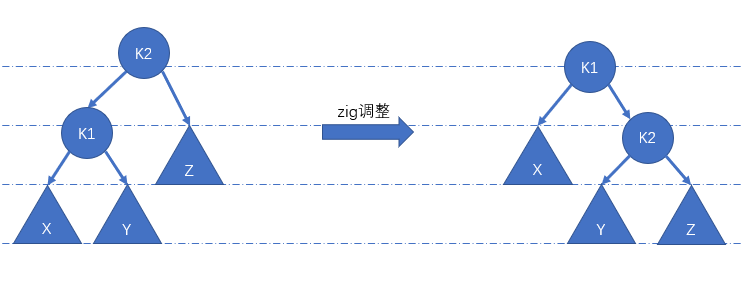

    图二：zig调整节点K1

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    private void zig(Node<E> root) {
        // 右旋要求当前节点为父节点的左儿子，不符合要求直接返回即可。
        if (root != root.parent.left) {
            return ;
        }

        Node<E> parent = root.parent;
        Node<E> grandParents = parent.parent;

        // 首先调整父节点的左儿子指向及对应左儿子的父节点指向。
        parent.left = root.right;
        if (null != root.right) {
            root.right.parent = parent;
        }

        // 其次调整当前节点的父节点指向及对应父节点的儿子指向。
        root.parent = grandParents;
        if (null != grandParents) {
            if (parent == grandParents.left) {
                grandParents.left = root;
            } else {
                grandParents.right = root;
            }
        }

        // 最后调整当前节点的右儿子指向及对应右儿子的父节点指向
        root.right = parent;
        parent.parent = root;
    }

  • zag

    通过 zag 调整使节点 K1 成为根节点。

    zag 调整与 AVL 中的 RR 基本相同，同为左旋。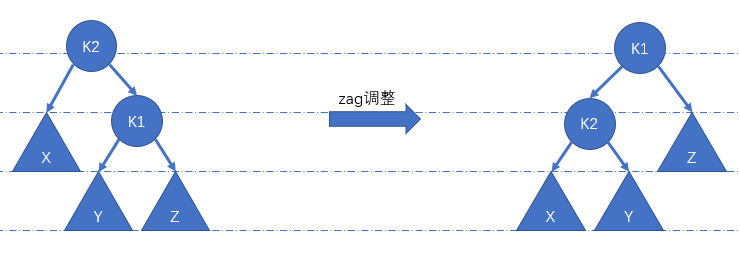

    图三：zag调整节点K1

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    private void zag(Node<E> root) {
        // 左旋要求root节点为父节点的右儿子，不符合要求直接返回即可。
        if (root != root.parent.right) {
            return ;
        }

        Node<E> parent = root.parent;
        Node<E> grandParents = parent.parent;

        // 首先调整父节点的右儿子指向及对应右儿子的父节点指向。
        parent.right = root.left;
        if (null != root.left) {
            root.left.parent = parent;
        }

        // 其次调整当前节点的父节点指向及对应父节点的儿子指向。
        root.parent = grandParents;
        if (null != grandParents) {
            if (parent == grandParents.left) {
                grandParents.left = root;
            } else {
                grandParents.right = root;
            }
        }

        // 最后调整当前节点的左儿子指向及对应左儿子的父节点指向。
        root.left = parent;
        parent.parent = root;
    }

  • zig-zig

    首先 zig 调整节点 K2，然后 zig 调整节点 K1，最终使得节点 K1 成为根节点。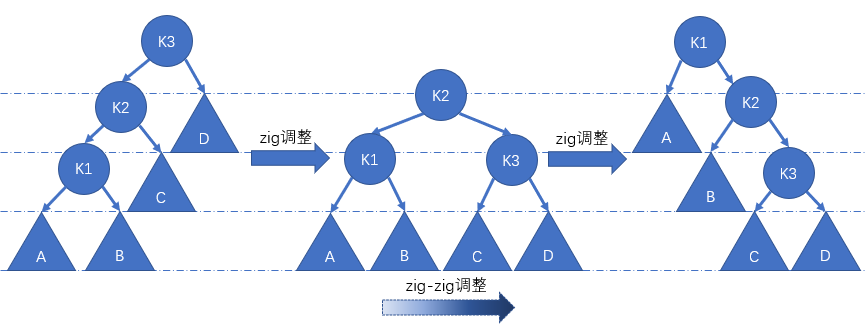

    图四：zig-zig调整节点K1

  • zag-zag

    首先 zag 调整节点 K2，然后 zag 调整节点 K1，最终使得节点 K1 成为根节点。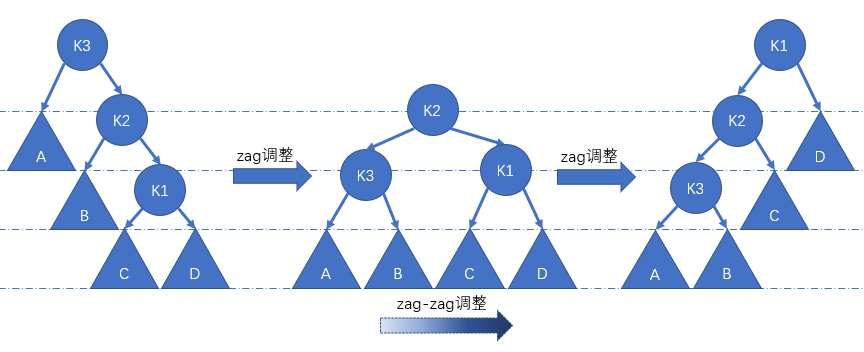

    图五：zag-zag调整节点K1

  • zig-zag

    首先 zig 调整节点 K1，然后 zag 调整节点 K1，最终使得节点 K1 成为根节点。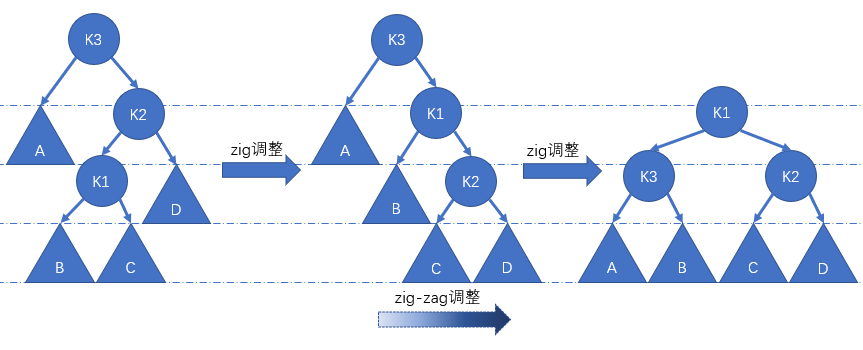

    图六：zig-zag调整节点K1

  • zag-zig

    首先 zag 调整节点 K1，然后 zig 调整节点 K1，最终使得节点 K1 成为根节点。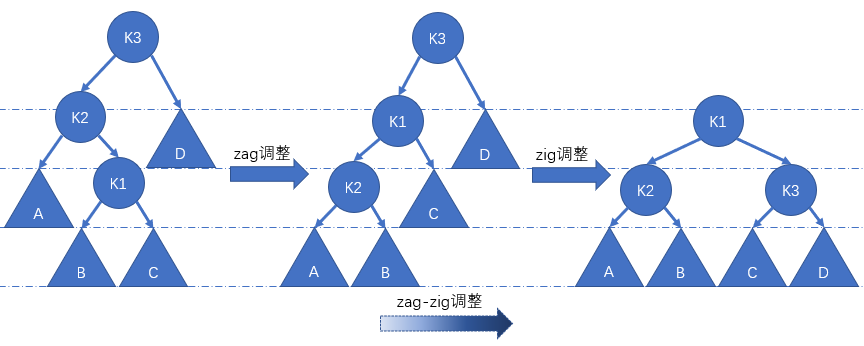

    图六：zag-zig调整节点K1

  • 伸展操作

    将节点 root 伸展到节点 target 的儿子节点处。

    伸展操作需使用到上述六大调整，此处代码对此作了些优化。 另外，当传入 target = null 时，需自行调整 root 指向。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    private void splay(Node<E> root, Node<E> target) {
        // 节点为空，无需伸展。
        if (null == root) {
            return ;
        }

        while (root.parent != target) {
            Node<E> parent = root.parent;

            if (root == parent.left) {
                // 表明当前节点为父节点的左儿子。

                // 祖父节点存在且父节点为祖父节点的左儿子，那么需要进行zig-zig调整，这种需要先调整父节点才能调整子节点。
                // 如果父节点为祖父节点的右儿子，那么需要进行zig-zag调整，这种属于先调整当前节点随后调整父节点，与当前代码流程相同，故而可不用处理。
                if (parent.parent != target && parent == parent.parent.left) {
                    zig(parent);
                }
                zig(root);
            } else {
                // 表明当前节点为父节点的右儿子。

                // 祖父节点存在且父节点为祖父节点的右儿子，那么需要进行zag-zag调整，这种需要先调整父节点才能调整子节点。
                // 如果父节点为祖父节点的左儿子，那么需要进行zag-zig调整。这种属于先调整当前节点随后调整父节点，与当前代码流程相同，故而可不用处理。
                if (parent.parent != target && parent == parent.parent.right) {
                    zag(parent);
                }
                zag(root);
            }
        }
    }

  • 当前子树中查找具有最小元素的节点

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    private Node<E> getMinTree(Node<E> root) {
        if (null == root) {
            return null;
        }

        Node<E> parent = root.parent;
        Node<E> node = root;
        while (null != node.left) {
            node = node.left;
        }
    	
        // 访问该节点，就需要将该节点进行伸展。
        splay(node, parent);
        return node;
    }

  • 当前子树中查找具有最大元素的节点

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    private Node<E> getMaxTree(Node<E> root) {
        if (null == root) {
            return null;
        }

        Node<E> parent = root.parent;
        Node<E> node = root;
        while (null != node.right) {
            node = node.right;
        }

        // 访问该节点，就需要将该节点进行伸展。
        splay(node, parent);
        return node;
    }

    初始化

1
2
3
public SplayTree(Comparator<? super E> comparator) {
    this.comparator = comparator;
}

查询

  • 查询指定元素是否存在

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    boolean contains(E item) {
        // 伸展树为空，直接返回false即可。
        if (null == this.root) {
            return false;
        }

        Node<E> node = this.root;
        while (null != node) {
            if (comparator.compare(node.item, item) > 0) {
                node = node.left;
            } else if (comparator.compare(node.item, item) == 0) {
                break;
            } else {
                node = node.right;
            }
        }

        if (null != node) {
            // 访问该节点，就需要将该节点进行伸展。
            // 伸展到null，需要调整 root 指向。
            splay(node, null);
            this.root = node;
            return true;
        } else {
            return true;
        }
    }

  • 查询最小元素

    1
    2
    3
    4
    E getMin() {
        this.root = getMinTree(this.root);
        return this.root.item;
    }

  • 查询最大元素

    1
    2
    3
    4
    E getMax() {
        this.root = getMaxTree(this.root);
        return this.root.item;
    }

    操纵

  • 伸展树中添加元素

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    public void add(E item) {
        // 伸展树为空，直接创建该结点即可。
        if (null == this.root) {
            this.root = new Node<>(item);
            return ;
        }

        // 伸展树不为空，向下查找并插入待插入值。
        Node<E> node = this.root;
        while (true) {
            // 当前节点值大于待插入值，则应在左子树中查找。
            if (comparator.compare(node.item, item) > 0) {
                if (null == node.left) {
                    node.left = new Node<>(item);
                    node.left.parent = node;
                    node = node.left;
                    break;
                } else {
                    node = node.left;
                }
            } else if (comparator.compare(node.item, item) == 0) {
                // 当前节点值等于待插入值，直接返回即可。
                return ;
            } else {
                // 当前节点值小于待插入值，则应在右子树中查找。
                if (null == node.right) {
                    node.right = new Node<>(item);
                    node.right.parent = node;
                    node = node.right;
                    break;
                } else {
                    node = node.right;
                }
            }
        }

        // 访问该节点，就需要将该节点进行伸展。
        // 伸展到null，需要调整 root 指向。
        splay(node, null);
        this.root = node;
    }

  • 伸展树中删除指定元素

    删除操作采用了比较高明的技巧。具体删除操作步骤如下：

    1. 查找该元素，如果存在则将其伸展至根节点，否则直接返回。
    2. 删除该节点后，将剩余左右两棵子树。如果一方为空，则指定另一方为根节点即可。
    3. 两方均不为空，找到左子树中具有最大元素的节点并将其旋转至根节点，那么可想而知：此时左子树的右儿子为空，直接将右子树置于此位置即可。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    public void delete(E item) {
        // 查找该元素，如果存在则会通过伸展将其置于根结点，否则直接返回即可。
        if (contains(item) == false) {
            return ;
        }

        // 至少一方为空。
        if (null == this.root.left && null == this.root.right) {
            this.root = null;
            return;
        }

        if (null == this.root.left) {
            this.root = this.root.right;
            this.root.parent = null;
            return;
        }

        if (null == this.root.right) {
            this.root = this.root.left;
            this.root.parent = null;
            return;
        }

        // 左右子树均不为空。
        // 获取左子树中最大节点，亦即当前根节点的前驱节点。
        Node<E> pre = getMaxTree(this.root.left);
        pre.parent = null;
        // 置前驱节点的右儿子为当前根节点的右儿子。
        pre.right = this.root.right;
        pre.right.parent = pre;
        // 调整root指向。
        this.root = pre;
    }

扩展

上面所示代码为自底向上实现伸展树，另外还可自顶向下实现伸展树。大致做法为：从根节点向叶子节点搜索过程中，依次构造三棵树：L 小于当前树中节点所构成的树，X 当前节点所在树，R 大于当前树中节点所构成的树。最后通过一定规则合并这三棵树，从而使得访问节点成为伸展树的根结点。

具体做法不再详述，该种方法相比于自底向上实现伸展树而言，优点就是无需存储父节点信息。

相关文章