数据结构-斐波那契堆

概述

斐波那契堆 属于一种构建极为精妙的堆。它由二项队列改造而成，并将懒惰合并及左式堆的 decreaseKey() 实现方法融入其中，最终造就除删除操作外的所有操作的平均时间复杂度为 $O(1)$。

其结构图大致如下：

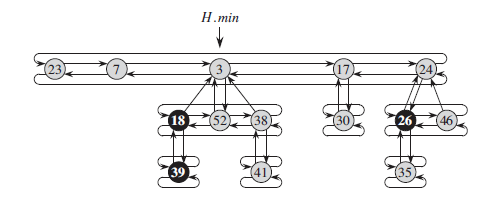
斐波那契堆是具有堆序结构的有根树的集合，该集合中允许具有相同高度的有根树同时存在。该有根树是一棵具有一定限制的树，而正是该种限制，使得有根树中节点数量 $N$ 与根结点的孩子节点数量 $R$ 间具有如下关系： $R = O(log^N)$ ，该关系保证了斐波那契堆之上所有操作的平均时间复杂度。

• 懒惰合并及左式堆的 decreaseKey() 实现方法见之前文章。
• 斐波那契堆理论上具有良好的性能，但是由于其编程复杂性及时间复杂度的常数因子过大，使得其并不常用。

结构

斐波那契堆中节点结构极其复杂，涉及四个节点引用，这也使得其编程较为复杂。

class FibonacciHeap<E> {
    // 节点结构
    static class Node<E> {
        // 具体元素
        E item;
        // 度(当前节点的孩子数目)
        int degree;
        // 自上次成为另一个节点的孩子以来，是否失去过孩子
        // 基于此字段对有根树施以限制。
        boolean mark;
        // 父亲节点
        Node<E> parent;
        // 某一个孩子节点
        Node<E> child;
        // 左兄弟
        Node<E> left;
        // 右兄弟
        Node<E> right;

        public Node(E item) {
            this.item = item;
            this.degree = 0;
            this.mark = false;
            this.parent = null;
            this.child = null;
            this.left = null;
            this.right = null;
        }
    }
    // 指向斐波那契堆最小节点,用以访问整个斐波那契堆
    private Node<E> min;
    // 堆中节点个数
    private int currentSize;
    // 比较函数
    private final Comparator<? super E> comparator;
}

实现

辅助方法

• 合并两个环形链表

  private void unionLinked(Node<E> e1, Node<E> e2) {
      e1.right.left = e2.left;
      e2.left.right = e1.right;
      e1.right = e2;
      e2.left = e1;
  }

• 从环形链表中剔除指定节点 (当前节点非环形链表中最后一个节点)

  private void deleteLinkedNode(Node<E> node) {
      node.left.right = node.right;
      node.right.left = node.left;
      node.left = null;
      node.right = null;
  }

• 向指定环形链表中添加指定节点

  private void addLinkedNode(Node<E> node, Node<E> root) {
      node.left = root.left;
      node.right = root;
      root.left = node;
      node.left.right = node;
  }

• 链接两棵有根树，将根值小者作为根值大者的孩子，并返回最终结果

  private Node<E> linkTree(Node<E> e1, Node<E> e2) {
      // 保证e1为根值小者，e2为根值大者。
      if (comparator.compare(e1.item, e2.item) > 0)
          return linkTree(e2, e1);
  
      // 如果e1孩子节点为空，则需调整以指向e2。
      if (null == e1.child) {
          e2.left = e2;
          e2.right = e2;
          e1.child = e2;
      } else {
          addLinkedNode(e2, e1.child);
      }
  
      // 更新其他信息
      // 按照上述mark定义，此处应当置为false。
      e2.parent = e1;
      e2.mark = false;
      e1.degree++;
      return e1;
  }

• 根链表有根树合并

  根链表指代 min 字段指向的那个环形链表。

  该部分做法与懒惰二项队列合并相同高度的二项树做法类似。具体步骤如下：

  1. 构建一个集合，用于存放含有不同度数的有根树。
  2. 每次从环形链表中取出一棵有根树，如果集合中存在相同度数的有根树则合并，否则直接将其置于集合中即可。
  3. 根据集合，构建出一个环形链表，将 min 字段指向最小节点即可。

  private void union() {
      // 估计有根树的最大度数。
      int rootNum = (int)Math.floor(Math.log(this.currentSize) / Math.log(2));
  
      // 初始化一个存放相同度数有根树集合。
      Node<E>[] trees = new Node[rootNum];
  
      // 每次从根链表中提取一个节点，将其置于有根树集合中。
      while (true) {
          Node<E> node1 = this.min.right;
          if (node1 == this.min) {
              break;
          }
          deleteLinkedNode(node1);
  
          int degree = node1.degree;
          // 如果链表集当前度数位置不为空，表明需进行合并。
          while (null != trees[degree]) {
              Node<E> node2 = trees[degree];
              node1 = linkTree(node1, node2);
              trees[degree] = null;
              degree++;
          }
          trees[degree] = node1;
      }
  
      // 将有根树集合中的树恢复为根链表，并更新min字段。
      for (int i = 0; i < trees.length; i++) {
          if (null == trees[i]) {
              continue;
          }
  
          if (null == this.min) {
              this.min = trees[i];
              this.min.left = this.min;
              this.min.right = this.min;
          } else {
              addLinkedNode(trees[i], this.min);
              this.min = comparator.compare(this.min.item, trees[i].item) > 0 ? trees[i] : this.min;
          }
      }
  }

  相关定理证明得到：斐波那契堆中有根树的最大度数 $D$ 与堆中节点数量 $N$ 之间具有如下关系：$D \leq \lfloor log_{\phi}^N \rfloor, \phi = (1 + \sqrt{5}) / 2 \approx 1.618$。

• 切除当前节点与父节点间关系，并将当前节点置于根链表之中

  private void cut(Node<E> node, Node<E> parent) {
      // 当前节点为父节点唯一节点，则需置空父节点的孩子节点指向，否则将该节点从父节点的孩子节点所在环形链表中删除即可。
      if (node.right == node) {
          parent.child = null;
      } else {
          deleteLinkedNode(node);
      }
      parent.degree--;
  
      // 将当前节点置于根链表之中。
      // 按照上述mark定义，此处应当置为false。
      addLinkedNode(node, this.min);
      node.parent = null;
      node.mark = false;
  }

• 级联切除

  通过 mark 字段判断是否需要及时将当前节点置于根链表之中，以保证有根树中节点数量 $N$ 与根结点的孩子节点数量 $R$ 之间的关系。

  private void cascadingCut(Node<E> node) {
      Node<E> parent = node.parent;
      if (null != parent) {
          // 如果当前节点为非根节点，且为第二次失去儿子节点，则应当将其与父节点断开，置于根链表之中。
          if (node.mark) {
              cut(node, parent);
              cascadingCut(parent);
          } else {
              // 那么这便是首次失去儿子节点，应当将mark置为true。
              node.mark = true;
          }
      }
  }

  初始化

public FibonacciHeap(Comparator<? super E> comparator) {
    this.comparator = comparator;
}

查询

• 查询最小元素

  public E getMin() {
      return null == this.min ? null : this.min.item;
  }

  操纵

• 斐波那契堆中添加元素

  直接将节点置于根链表之中即可。

  public void insert(E item) {
      Node<E> node = new Node<>(item);
      if (null == this.min) {
          // 将当前节点构成一个双向链表
          node.left = node;
          node.right = node;
  
          // 设置最小节点指向
          this.min = node;
      } else {
          // 将当前节点插入到根链表之中
          addLinkedNode(node, this.min);
  
          // 如果当前节点比最小节点小，则需更新
          this.min = comparator.compare(this.min.item, node.item) < 0 ? this.min : node;
      }
      this.currentSize++;
  }

• 斐波那契堆合并

  直接将两者根链表合并即可。

  public void merge(FibonacciHeap<E> fibonacciHeap) {
      // 待合并堆为空，或者待合并堆就是当前堆，直接返回即可
      if (null == fibonacciHeap.min || fibonacciHeap == this) {
          return ;
      }
  
      // 如果当前堆为空，则直接将待合并堆赋值给当前堆即可
      if (null == this.min) {
          this.min = fibonacciHeap.min;
          this.currentSize = fibonacciHeap.currentSize;
          return ;
      }
  
      // 二者皆不为空，先合并根链表，然后更新最小节点
      this.min = unionLinked(this.min, fibonacciHeap.min);
  
      this.min = comparator.compare(this.min.item, fibonacciHeap.min.item) > 0 ? fibonacciHeap.min : this.min;
      this.currentSize = this.currentSize + fibonacciHeap.currentSize;
  }

• 斐波那契堆中指定节点降低元素值

  具体实现与左式堆中 decreaseKey() 操作实现类似。如果指定节点降低元素值后当前有根树不满足堆序性质，则将当前节点所在子树置于根链表之中，同时调整当前有根树。

  public void decreaseKey(Node<E> node, E item) {
      // 如果待赋值大于当前节点值，直接返回即可。
      if (comparator.compare(node.item, item) < 0) {
          return ;
      }
  
      node.item = item;
  
      Node<E> parent = node.parent;
      // 当前节点父节点不为空，表明非有根树的根结点。另外如果减值后值小于父节点值，则需要进行调整以保证堆序
      if (null != parent && comparator.compare(node.item, parent.item) < 0) {
          // 将当前节点从父节点中清除，并置于根链表之中。
          cut(node, parent);
  
          // 级联切除
          cascadingCut(parent);
      }
      // 减值后的值小于最小节点值，则应当更新最小节点。
      if (comparator.compare(node.item, this.min.item) < 0) {
          this.min = node;
      }
  }

• 斐波那契堆中删除最小节点

  删除最小节点后，可能根链表中有根树过多，此时需要进行一次集中合并。

  public E deleteMin() {
      // 当前堆为空，直接返回空即可。
      if (null == this.min) {
          return null;
      }
  
      Node<E> deleteNode = this.min;
  
      // 待删除节点存在孩子节点，则将其置于当前堆的根链表之中
      if (null != deleteNode.child) {
          Node<E> tmp = deleteNode.child;
          while (null != tmp) {
              tmp.parent = null;
              tmp = tmp.right == deleteNode.child ? null : tmp.right;
          }
          this.min = unionLinked(this.min, deleteNode.child);
          deleteNode.child = null;
      }
  
      // 从当前堆中移除该节点
      if (deleteNode.right == deleteNode) {
          // 堆中仅有这一个节点，移除后置空最小节点
          this.min = null;
      } else {
          // 这里更新最小节点，并指向待删除节点的右兄弟。此时最小节点指向不需要一定正确，后续会进行union操作。
          this.min = deleteNode.right;
  
          // 从根链表中删除最小节点
          deleteLinkedNode(deleteNode);
  
          // 删除最小节点使得根链表中节点过多，因此需要整理，顺便找到最小节点。
          union();
      }
  
      this.currentSize--;
      return deleteNode.item;
  }

• 斐波那契堆中删除指定节点

  具体操作可通过上面两个操作加以实现。

  public void delete(Node<E> node) {
      decreaseKey(node, this.min.item);
      this.min = node;
      deleteMin();
  }