数据结构-并查集

发表于 分类于
本文字数： 1.5k 阅读时长 ≈ 1 分钟

概述

并查集 是一种基于双亲表示法表示的森林。它以一棵树表示一个集合，进而处理不相交集合的合并、查询问题。

其结构图大致如下：

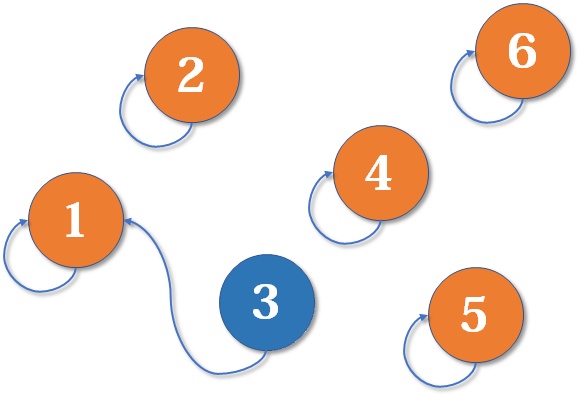
图一：并查集

针对并查集中的合并、查询操作有多种优化手段，我们在此提前介绍，并且仅展示优化后的代码。

  • 针对合并操作的优化

    • 按大小求并：总让含有较少元素的树成为含有较多元素的树的子树。
    • 按高度求并：总让高度较低的树成为高度较高的树的子树。

  • 针对查询操作的优化

    • 路径压缩：将查找点到根结点的路径上所有结点的父节点直接指定为根结点。

  • 综合合并、查询优化

    按大小求并与路径压缩二者可同时实现，而按高度求并与路径压缩并不能同时实现，原因在于：路径压缩会破坏树的高度。由于此时节点存储的高度信息实际上为预估高度，故而称此时的按高度求并为按秩求并。

    实际中大多数并查集都是基于按秩求并与路径压缩实现的。

经优化后，并查集各种操作的平均时间复杂度为 $O(1)$，证明过程十分麻烦，故不赘述。

结构

如上所述，并查集基于双亲表示法实现，故而使用数组最为合适。另外，本文仅考虑位置间合并、查询操作，而不考虑元素间合并、查询操作，毕竟通过散列表可将后者转换为前者。

1
2
3
4
5
6
7
8
9
10
11
class UnionFind {
    // 节点结构
    private static class Node {
        // 父节点
        int parent;
        // 秩(预估高度)
        int rank;
    }
    // 节点集
    private Node[] nodes;
}

实现

初始化

各个位置自成一棵树，并使用根结点位置标识这一棵树。另外根据当前节点的父节点是否就是它自己，即可判断当前节点是否为所在树的根节点。

1
2
3
4
5
6
7
public UnionFind() {
    nodes = new Node[10];
    for (int i = 0; i < 10; i++) {
        nodes[i].parent = i;
        nodes[i].rank = 0;
    }
}

查询

1
2
3
4
5
6
7
8
9
10
public int find(int index) {
    // 表明为根节点，返回标识
    if (index == this.nodes[index].parent) {
        return index;
    }
    // 路径压缩
    int root = find(this.nodes[index].parent);
    this.nodes[index].parent = root;
    return root;
}

合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public boolean union(int index1, int index2) {
    int root1 = find(index1);
    int root2 = find(index2);
    // 如果二者具有相同的树标识，表明二者是在同一棵树中，无需合并。
    if (root1 == root2) {
        return false;
    }

    // 按秩求并。
    if (this.nodes[root1].rank < this.nodes[root2].rank) {
        this.nodes[root1].parent = root2;
    } else if (this.nodes[root1].rank < this.nodes[root2].rank) {
        this.nodes[root2].parent = root1;
    } else {
        this.nodes[root1].parent = root2;
        this.nodes[root1].rank++;
    }
    return true;
}
相关文章