数据结构-平衡二叉树

发表于 分类于
本文字数： 5.9k 阅读时长 ≈ 5 分钟

概述

AVL (平衡二叉树) 是一种自平衡的二叉查找树。该平衡条件为：对于每个节点而言，左右子树的高度差不超过 1。

其结构图大致如下：

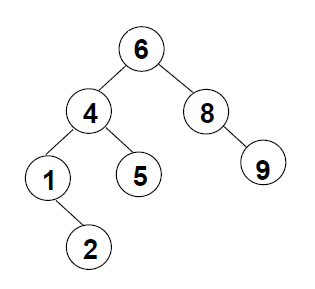
图一：平衡二叉树

平衡二叉树所涉操作的代码实现与二叉查找树基本相同，但是由于插入、删除操作可能破坏平衡条件，故而这两个操作需要一定额外代码以恢复平衡。为精简篇幅，本文仅展示插入、删除操作的代码实现。

结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class AVL<E> {
    // 节点结构
    private static class Node<E> {
        // 具体元素
        E item;
        // 左儿子
        Node<E> left;
        // 右儿子
        Node<E> right;
        // 当前子树的高度
        int height;

        public Node(E item, Node<E> left, Node<E> right, int height) {
            this.item = item;
            this.left = left;
            this.right = right;
            this.height = height;
        }
    }
    // 比较函数
    private final Comparator<? super E> comparator;
    // 根节点
    private Node<E> root;
}

实现

辅助方法

  • 获取节点高度

    空节点高度指定为 -1，方便后面编码。

    1
    2
    3
    private int height(Node<E> node) {
        return null == node ? -1 : node.height;
    }

  • 调整节点高度

    1
    2
    3
    4
    5
    6
    private void reHeight(Node<E> node) {
        if (null == node) {
            return;
        }
        node.height = Math.max(height(node.left), height(node.right)) + 1;
    }

  • 当前子树中查找最小元素

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    private E getMinTree(Node<E> root) {
        // 当前子树为空，直接返回空节点即可。
        if (null == root) {
            return null;
        }

        if (null == root.left) {
            // 当前子树根节点的左儿子为空，表明这是最左节点，此一定为最小元素，故直接返回之。
            return root.item;
        } else {
            // 当前子树根节点的左儿子不为空，则在左子树中查找最小元素。
            return getMinTree(root.left);
        }
    }

  • 当前子树中查找最大元素

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    private E getMaxTree(Node<E> root) {
        // 当前子树为空，直接返回空节点即可。
        if (null == root) {
            return null;
        }

        if (null == root.right) {
            // 当前子树根节点的右儿子为空，表明这是最右节点，此一定为最大元素，故直接返回之。
            return root.item;
        } else {
            // 当前子树根节点的右儿子不为空，则在右子树中查找最大元素。
            return getMaxTree(root.right);
        }
    }

  • 调整操作

    向树中插入元素时，从插入点到根节点的路径上的所有节点的平衡条件都有可能被破坏，因为只有它们的子树可能发生变化。

    从插入点沿该路径上行到根节点的过程中，我们称第一个平衡条件被破坏的节点为 $\alpha$ 。实践证明：通过调整 $\alpha$， 不仅可使得 $\alpha$ 满足平衡条件，同时可保证该路径上的其他节点也都满足平衡条件。接下来我们将详细讲述如何调整？

    由平衡二叉树定义可知，平衡条件被破坏意指 $\alpha$ 的左右子树高度差为 2。具体可分为两种情况，如图二所示 ( $K2$ 指代 $\alpha$，较高子树高度比较低子树高度大 2 )：

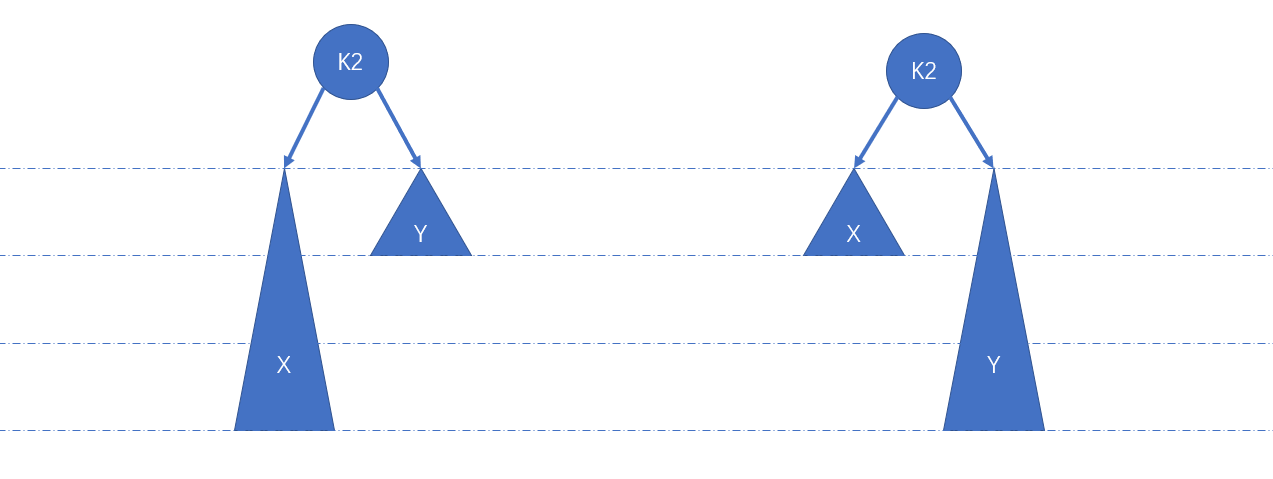
    图二：平衡条件被破坏的两种情况

    依据上图无法实施调整，因此可进一步细化为下图 ( $K2$ 指代 $\alpha$，两个较低子树具有相同高度，较高子树高度比较低子树高度大 1 )：

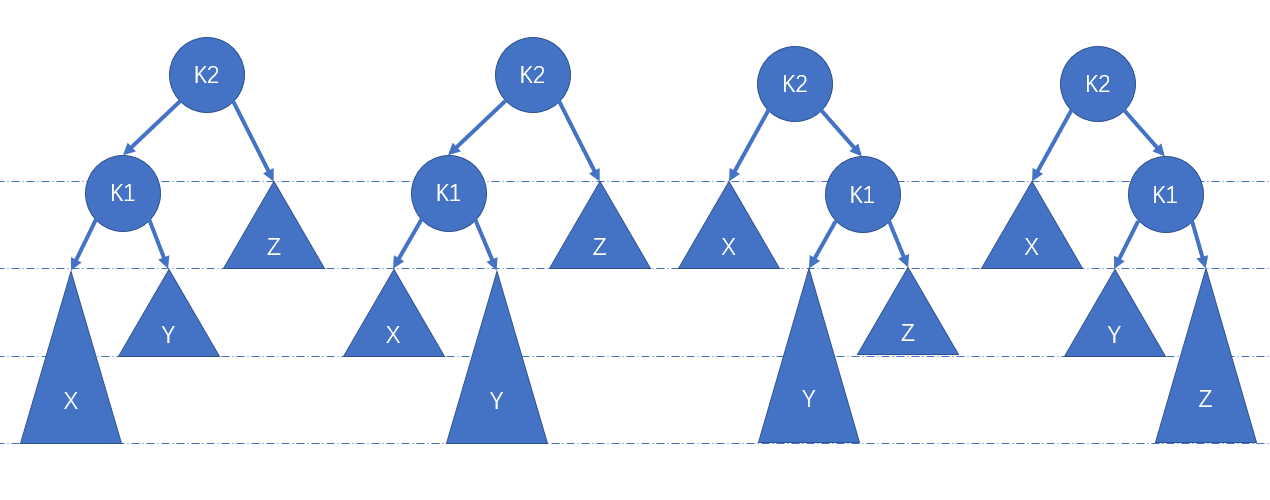
    图三：平衡条件被破坏的四种情况

    该图从左到右四种情况，我们依次称之为：对 $\alpha$ 的左儿子的左子树进行一次插入 (LL)、对 $\alpha$ 的左儿子的右子树进行一次插入 (LR)、对 $\alpha$ 的右儿子的左子树进行一次插入 (RL)、对 $\alpha$ 的右儿子的右子树进行一次插入 (RR)。

    情况一、四可通过对树的一次 单旋转 而完成调整，情况二、三则需要通过稍微复杂的 双旋转 完成调整。

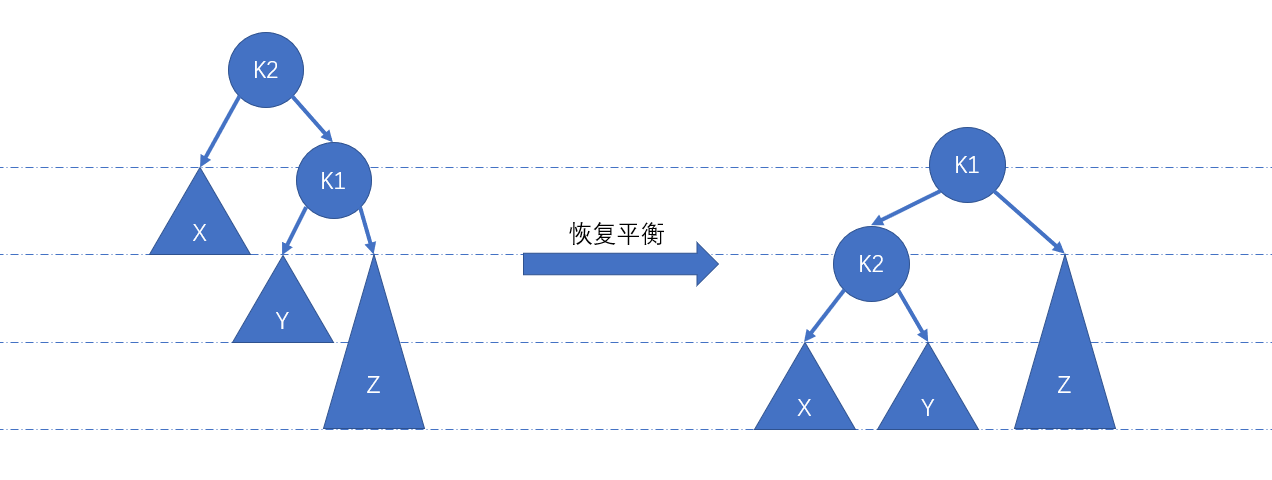
    单旋转：

    • LL

      调整方法如下：

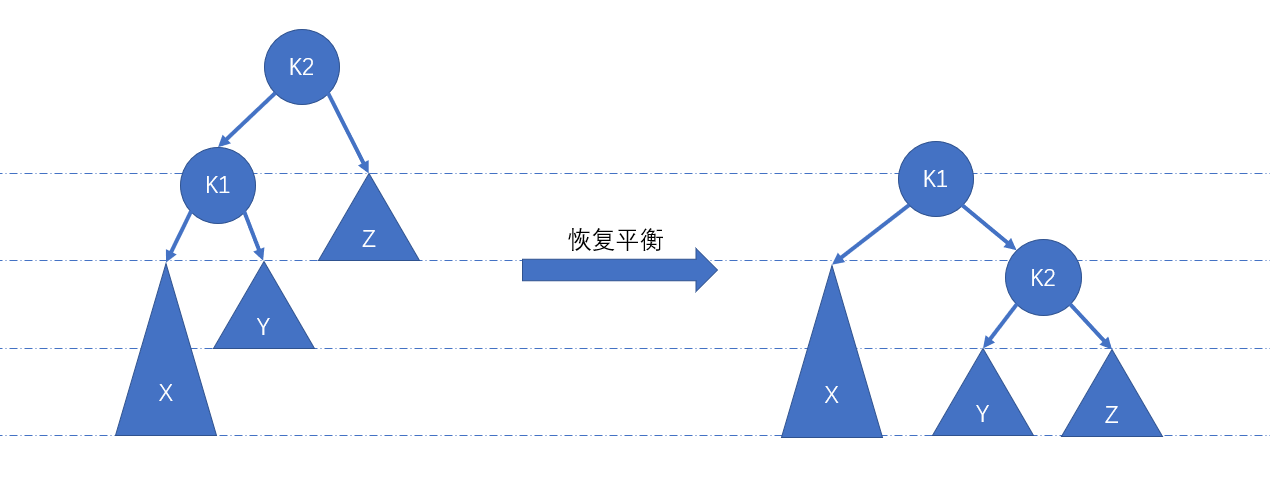
      图四：LL调整

      1
      2
      3
      4
      5
      6
      7
      8
      9
      private Node<E> LL(Node<E> root) {
          Node<E> k1 = root.left;
          Node<E> k2 = root;
          k2.left = k1.right;
          k1.right = k2;
              reHeight(k1);
          reHeight(k2);
              return k1;
      }

    • RR

      调整方法如下：

      图五：RR调整

      1
      2
      3
      4
      5
      6
      7
      8
      9
      private Node<E> RR(Node<E> root) {
          Node<E> k1 = root.right;
          Node<E> k2 = root;
          k2.right = k1.left;
          k1.left = k2;
          reHeight(k1);
          reHeight(k2);
          return k1;
      }

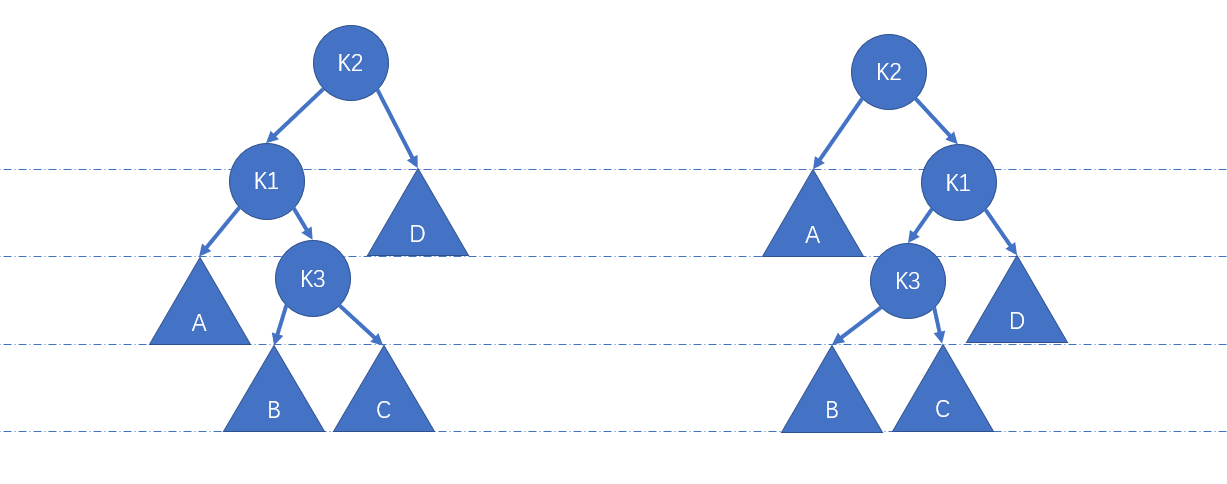
    双旋转：

    依据图三无法针对情况二、三进行调整，故而对情况二、三进一步细化：

    图六：细化LR与RL

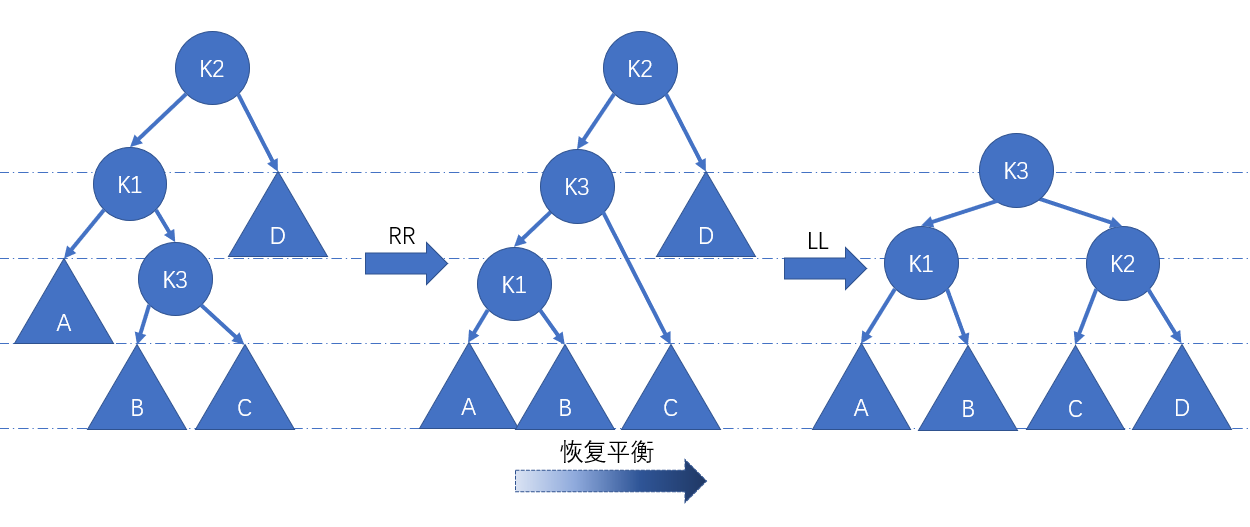
    • LR

      调整方法如下：

      图七：LR调整

      1
      2
      3
      4
      5
      private Node<E> LR(Node<E> root) {
          root.left = RR(root.left);
          root = LL(root);
          return root;
      }

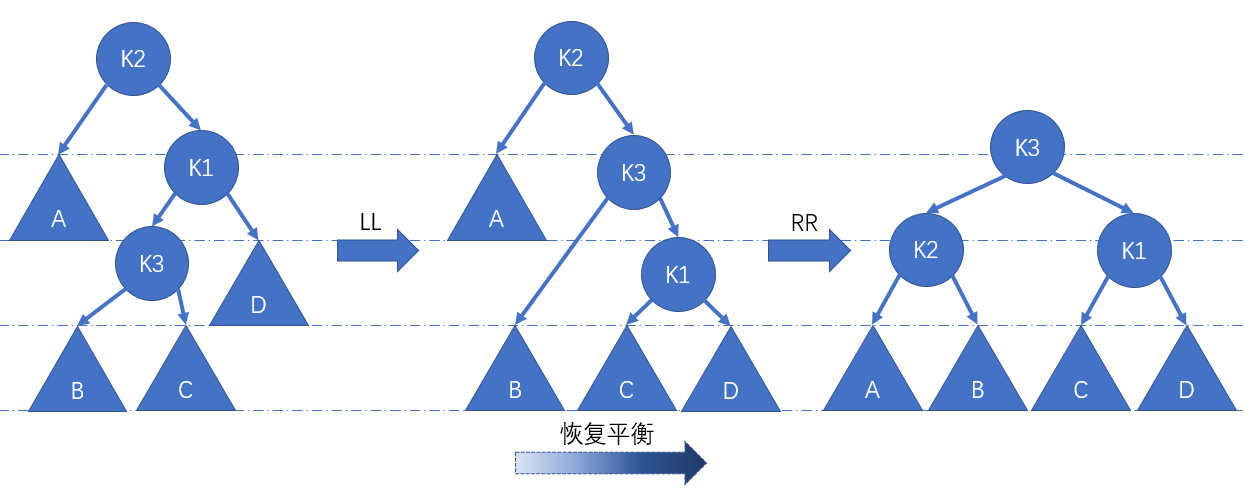
    • RL

      调整方法如下：

      图八：RL调整

      1
      2
      3
      4
      5
      private Node<E> RL(Node<E> root) {
          root.right = LL(root.right);
          root = RR(root);
          return root;
      }
      • 细化依据：平衡条件被破坏意指 $\alpha$ 的左右子树高度差为 2。那么高度较高的子树一定可以提取出一个儿子节点和一个孙子节点。
      • 我们知道：插入元素最多可使得子树高度增加一。故而原先保持平衡条件的子树高度比平衡条件被破坏后的子树高度小一。另外观察四种情况的恢复平衡图，可以发现恢复平衡后子树高度比平衡条件被破坏后子树高度小一。综合二者可得到如下结论：原先保持平衡条件的子树高度与恢复平衡后子树高度相同。既然相同，从 $\alpha$ 上行到根节点的路径上的所有节点的平衡条件自然无需再做调整。

  • 当前子树中插入元素，并返回插入元素后的该子树

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    private Node<E> addTree(Node<E> root, E item) {
        if (null == root) {
            // 向空树中插入元素，直接返回该元素即可。
            return new Node<>(item, null, null, 0);
        }
        if (comparator.compare(root.item, item) > 0) {
            // 当前子树根节点值大于指定元素，表明应当插于左子树之中。
            root.left = addTree(root.left, item);
            // 插入可能导致平衡条件被破坏，应当进行适当调整
            if (height(root.left) - height(root.right) == 2) {
                if (height(root.left.left) > height(root.left.right)) {
                    // 左儿子的左子树高度高于左儿子的右子树，对应情况一。
                    root = LL(root);
                } else {
                    // 左儿子的左子树高度低于左儿子的右子树，对应情况二。
                    root = LR(root);
                }
            }
        } else if (comparator.compare(root.item, item) < 0) {
            // 当前子树根节点值小于指定元素，表明应当插于右子树之中。
            root.right = addTree(root.right, item);
            // 插入可能导致平衡条件被破坏，应当进行适当调整
            if (height(root.right) - height(root.left) == 2) {
                if (height(root.right.right) > height(root.right.left)) {
                    // 右儿子的右子树高度高于右儿子的左子树，对应情况四。
                    root = RR(root);
                } else {
                    // 右儿子的右子树高度低于右儿子的左子树，对应情况三。
                    root = RL(root);
                }
            }
        }

        reHeight(root);
        return root;
    }

  • 当前子树中删除指定元素，并返回删除指定元素后的该子树

    删除策略与二叉查找树中采取的策略大致相同。另外，通过将删除操作等价于添加操作，实现借用上述四种情况实施调整以恢复平衡条件。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    private Node<E> deleteTree(Node<E> root, E item) {
        // 当前子树根节点为空，直接返回空即可。
        if (null == root) {
            return null;
        }

        if (comparator.compare(root.item, item) > 0) {
            // 当前子树根节点值大于给定元素，则待删除元素一定位于左子树。
            root.left = deleteTree(root.left, item);
            // 删除可能导致平衡条件被破坏，应当进行适当调整
            // 向当前子树的左子树删除一个元素等价于向当前子树的右子树中添加一个元素，因此失衡条件判断应当为当前子树的右子树高度比当前子树的左子树高度大2。
            if (height(root.right) - height(root.left) == 2) {
                if (height(root.right.right) > height(root.right.left)) {
                    // 右儿子的右子树高度高于右儿子的左子树，对应情况四。
                    root = RR(root);
                } else {
                    // 右儿子的右子树高度低于右儿子的左子树，对应情况三。
                    root = RL(root);
                }
            }
        } else if (comparator.compare(root.item, item) < 0) {
            // 当前子树根节点值小于给定元素，则待删除元素一定位于右子树。
            root.right = deleteTree(root.right, item);
            // 删除可能导致平衡条件被破坏，应当进行适当调整
            // 向当前子树的右子树删除一个元素等价于向当前子树的左子树添加一个元素，因此失衡条件判断应当为当前子树的左子树高度比当前子树的右子树高度大2。
            if (height(root.left) - height(root.right) == 2) {
                if (height(root.left.left) > height(root.left.right)) {
                    // 左儿子的左子树高度高于左儿子的右子树，对应情况一。
                    root = LL(root);
                } else {
                    // 左儿子的左子树高度低于左儿子的右子树，对应情况二。
                    root = LR(root);
                }
            }
        } else {
            // 当前元素就是待删除元素
            // 左右儿子其中一者为空，直接将另一者所在子树作为当前子树，这种操作并不会使得平衡条件被破坏，因此无需调整。
            if (null == root.left) {
                root = root.right;
            } else if (null == root.right) {
                root = root.left;
            } else {
                // 删除元素最多使得当前子树高度差增加一。这里采取从高度较高的子树中删除一个元素，即使使得高度差增加一，也不会使当前子树根节点的平衡条件被破坏。
                // 左右儿子节点均不为空。采取与二叉查找树删除操作类似做法，但是有所改进。
                if (height(root.left) > height(root.right)) {
                    // 当前子树的左子树更高，则找到当前子树左子树的最大值，将其与当前元素交换后，删除当前子树左子树的最大值即可。
                    root.item = getMaxTree(root.left);
                    root.left = deleteTree(root.left, root.item);
                } else {
                    // 当前子树的右子树更高，则找到当前子树右子树的最小值，将其与当前元素交换后，删除当前子树右子树的最小值即可。
                    root.item = getMinTree(root.right);
                    root.right = deleteTree(root.right, root.item);
                }
            }
        }

        reHeight(root);
        return root;
    }

初始化

1
2
3
public AVL(Comparator<? super E> comparator) {
    this.comparator = comparator;
}

操纵

  • 树中添加元素

    1
    2
    3
    public void add(E item) {
        this.root = addTree(this.root, item);
    }

  • 树中删除指定元素

    1
    2
    3
    public void delete(E item) {
        this.root = deleteTree(this.root, item);
    }
相关文章