数据结构-二叉树

发表于 2020-06-03 分类于数据结构与算法

本文字数： 5.4k 阅读时长 ≈ 5 分钟

概述

二叉树 是一种特殊的树，其中每个节点至多具有两个儿子节点。本文仅探讨 “树” 中最基本的操作——构建和遍历。

其结构图大致如下：

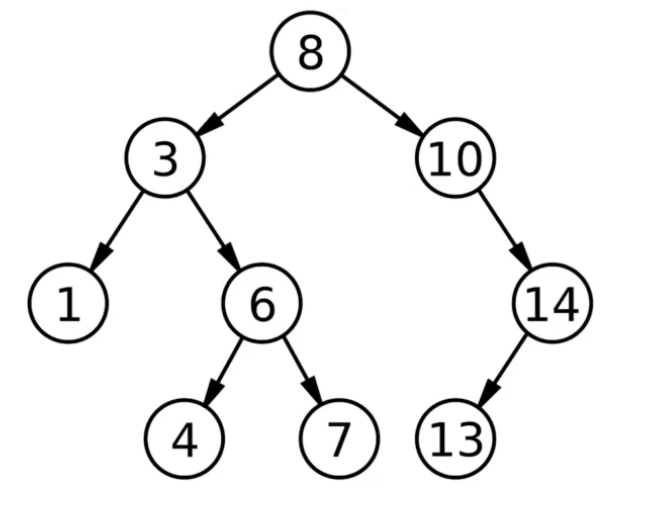
图一：二叉树

本文为 “树” 的第一篇文章，故而在此总结一下有关 “树” 的表示方法。

双亲表示法

借用一组连续/离散空间来存储 “树” 中节点。在保存节点内容的同时，还保存一个指向双亲节点的指针元素。

应用举例：并查集。
孩子表示法

借用一组连续/离散空间来存储 “树” 中节点。在保存节点内容的同时，还保存若干指向孩子节点的的指针元素。

应用举例：二叉查找树。
孩子兄弟表示法

借用一组连续/离散空间来存储 “树” 中节点。在保存节点内容的同时，还保存有两个指针元素，其中一个指针指向第一个孩子节点，另一个指针指向兄弟节点。

应用举例：二项队列。

结构

本文使用孩子表示法以表示二叉树。

class BinaryTree<E> {
    // 节点结构
    private static class Node<E> {
        // 具体元素
        E item;
        // 左儿子
        Node<E> left;
        // 右儿子
        Node<E> right;

        public Node(E item, Node<E> left, Node<E> right) {
            this.item = item;
            this.left = left;
            this.right = right;
        }
    }
    // 根节点
    private Node<E> root;
    // 索引(用于构建二叉树)
    private int index;
}

实现

辅助方法

前序遍历构建二叉树

private Node<E> treePreOrder(E[] arr) {
    E element = arr[this.index++];
    if (null == element) {
        return null;
    }
    Node<E> root = new Node<>(element, null, null);
    root.left = treePreOrder(arr);
    root.right = treePreOrder(arr);
    return root;
}

层序遍历构建二叉树

private Node<E> treeLevelOrder(E[] arr) {
    if (arr.length == 0) {
        return null;
    }
    int index = 0;
    Node<E> root = new Node<>(arr[index++], null, null);
    
    // 使用双端队列模拟队列
    ArrayDeque<Node<E>> queue = new ArrayDeque<>();
    queue.addLast(root);

    while (queue.size() > 0) {
        Node<E> tmp = queue.pollFirst();
        E left = arr[index++];
        E right = arr[index++];
        if (null != left) {
            tmp.left = new Node<>(left, null, null);
            queue.addLast(tmp.left);
        }
        if (null != right) {
            tmp.right = new Node<>(right, null, null);
            queue.addLast(tmp.right);
        }
    }
    return root;
}

前序遍历二叉树

private void traverseTreePreOrder(final Node<E> root) {
    if (null == root) {
        return ;
    }
    System.out.print(root.item + " ");
    traverseTreePreOrder(root.left);
    traverseTreePreOrder(root.right);
}

中序遍历二叉树

private void traverseTreeInOrder(final Node<E> root) {
    if (null == root) {
        return ;
    }
    traverseTreeInOrder(root.left);
    System.out.print(root.item + " ");
    traverseTreeInOrder(root.right);
}

后序遍历二叉树

private void traverseTreePostOrder(final Node<E> root) {
    if (null == root) {
        return ;
    }
    traverseTreePostOrder(root.left);
    traverseTreePostOrder(root.right);
    System.out.print(root.item + " ");
}

初始化

基于前序遍历、后序遍历和层序遍历的遍历结果，均可实现构建一棵二叉树。后序遍历顺序为 “左右根”，反向查看后序遍历的遍历结果，其遍历顺序便是 “根右左”，故而其与基于前序遍历的遍历结果构建一棵二叉树类似。

无法基于中序遍历构建一棵二叉树，原因在于：遍历过程中存在 “节点跳跃”。举例如下 (二者具有相同的中序遍历结果)：

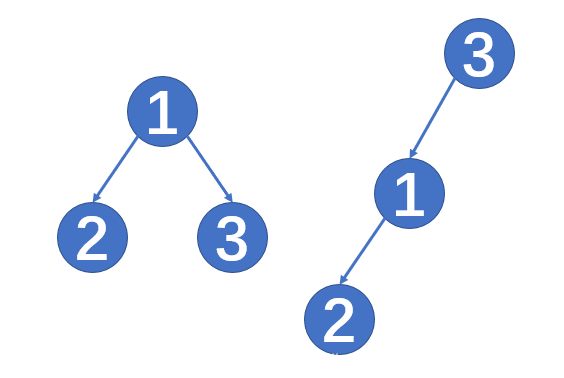
图二：中序遍历构建二叉树冲突

实际使用中，基本上也不会以这种方式构建二叉树。通常都是基于插入操作构建二叉树的。

public BinaryTree(E[] arr, int option) {
    if (option == 0) {
        this.root = treePreOrder(arr);
    } else {
        this.root = treeLevelOrder(arr);
    }
}

查询

前中后序遍历的非递归版本都十分难写，但可喜的是，三者具有一种统一的写法，具体见代码。

前序遍历 (递归)

public void traversePreOrder() {
    System.out.print("前序遍历（递归）：");
    traverseTreePreOrder(this.root);
    System.out.println("");
}

前序遍历 (非递归)

public void traversePreOrderStack() {
    Node<E> node = this.root;
    // 使用双端队列模拟栈
    ArrayDeque<Node<E>> stack = new ArrayDeque<>();

    System.out.print("前序遍历（非递归）：");
    while ((null != node) || (stack.size() > 0)) {
        while (null != node) {
            System.out.print(node.item + " ");
            stack.addLast(node);
            node = node.left;
        }
        if (stack.size() > 0) {
            node = stack.pollLast();
            node = node.right;
        }
    }
    System.out.println("");
}

中序遍历 (递归)

public void traverseInOrder() {
    System.out.print("中序遍历（递归）：");
    traverseTreeInOrder(this.root);
    System.out.println("");
}

中序遍历 (非递归)

public void traverseInOrderStack() {
    Node<E> node = this.root;
    // 使用双端队列模拟栈
    ArrayDeque<Node<E>> stack = new ArrayDeque<>();

    System.out.print("中序遍历（非递归）：");
    while ((null != node) || (stack.size() > 0)) {
        while (null != node) {
            stack.addLast(node);
            node = node.left;
        }
        if (stack.size() > 0) {
            node = stack.pollLast();
            System.out.print(node.item + " ");
            node = node.right;
        }
    }
    System.out.println("");
}

后序遍历 (递归)

public void traversePostOrder() {
    System.out.print("后序遍历（递归）：");
    traverseTreePostOrder(this.root);
    System.out.println();
}

后序遍历 (非递归)

后序遍历顺序为 “左右根”，故而只有当左子树和右子树遍历完成后，才可遍历根节点。后序遍历的非递归版本难点在于：判断当前栈顶元素的右子树是否已遍历完成？

可使用一个指针以解决该问题，其中该指针指向上一个遍历过的元素。

public void traversePostOrderStack() {
    Node<E> node = this.root;
    // 记录上一个遍历过的节点
    Node<E> pre = null;
    // 使用双端队列模拟栈
    ArrayDeque<Node<E>> stack = new ArrayDeque<>();

    System.out.print("后序遍历（非递归）：");
    while ((null != node) || (stack.size() > 0)) {
        while (null != node) {
            stack.addLast(node);
            node = node.left;
        }
        if (stack.size() > 0) {
            node = stack.getLast();
            // 当前节点右子树为空或当前节点的右儿子为上一个遍历过的节点，表明右子树已遍历完成。此时即可遍历当前节点。
            if ((null == node.right) || (node.right == pre)) {
                System.out.print(node.item + " ");
                stack.pollLast();
                pre = node;
                node = null;
            } else {
                node = node.right;
            }
        }
    }
    System.out.println("");
}

层序遍历

public void traverseLevelOrder() {
    if (null == this.root) {
        return ;
    }
    
    // 使用双端队列模拟队列
    ArrayDeque<Node<E>> queue = new ArrayDeque<>();
    queue.addLast(this.root);

    System.out.print("层序遍历：");
    while (queue.size() > 0) {
        Node<E> tmp = queue.pollFirst();
        System.out.print(tmp.item + " ");
        if (null != tmp.left) {
            queue.addLast(tmp.left);
        }
        if (null != tmp.right) {
            queue.addLast(tmp.right);
        }
    }
    System.out.println(" ");
}