数据结构-散列表

发表于 分类于
本文字数： 2k 阅读时长 ≈ 2 分钟

概述

散列表 是一种可实现以常数平均时间执行插入、删除、查询的数据结构。它基于散列函数将元素映射到固定空间中的某一位置。

其结构图大致如下：

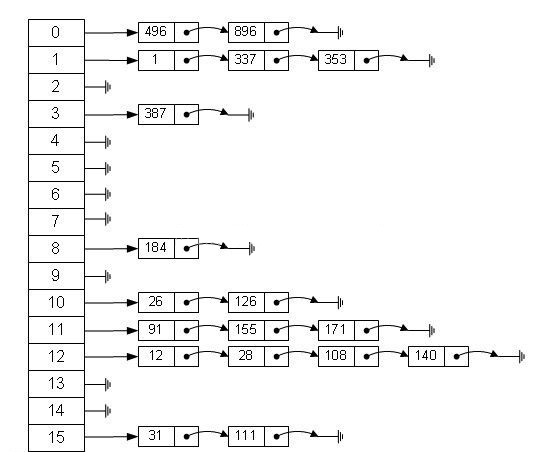
图一：散列表

散列表中有两大概念，在此先行解释。

  • 散列函数

    顾名思义，它就是一个函数，形如 $hash(key)$。其中 $key$ 表示元素键值，$hash(key)$ 表示经散列函数计算得到的散列值。

    散列函数的选择对于散列表性能具有重大影响。一个好的散列函数，可保证元素均匀分布于散列表之中。

  • 冲突

    散列表本质是将无穷元素映射到有穷空间之上。故而一定存在某两个元素键值不同，而具有相同的散列值，此种便称为冲突。

为解决 “冲突发生时如何映射元素” 这一问题，不同的散列表实现给出了不同的策略。我们主要展示基于链地址法实现的散列表，其余实现方法在 扩展 中简单介绍。

结构

基于链地址法实现散列表，故而固定数组存储内容为一个链表。另外数组大小应为一个素数，这样做有助于元素均匀分布于散列表。

1
2
3
4
5
6
7
8
class HashTable<E> {
    // 默认表长
    public static final int DEFAULT_TABLE_SIZE = 101;
    // 基于链地址法的散列表
    private LinkedList<E>[] lls;
    // 元素数量
    private int currentSize;
}

实现

辅助方法

  • 散列函数

    借用 $Object.hashCode()$ 加以实现。

    1
    2
    3
    4
    private int hash(E e) {
        int hashVal = e.hashCode() % this.lls.length;
        return (hashVal + this.lls.length) % this.lls.length;
    }

    初始化

1
2
3
4
5
6
public HashTable() {
    this.lls = new LinkedList[HashTable.DEFAULT_TABLE_SIZE];
    for (int i = 0; i < this.lls.length; i++) {
        this.lls[i] = new LinkedList<>();
    }
}

查询

  • 查询元素是否存在

    首先使用散列函数定位到链，然后在该链中查找该元素。

    1
    2
    3
    4
    5
    public boolean contains(E e) {
        // 获取待查询链
        LinkedList<E> link = this.lls[hash(e)];
        return link.indexOf(e) != -1;
    }

    操纵

  • 散列表中添加元素

    首先使用散列函数定位到链，当该元素并不存在于散列表中才插入。

    1
    2
    3
    4
    5
    6
    7
    8
    public void insert(E e) {
        // 获取待插入链
        LinkedList<E> link = this.lls[hash(e)];
        if (link.indexOf(e) == -1) {
            link.addFirst(e);
            this.currentSize++;
        }
    }

  • 散列表中删除元素

    首先使用散列函数定位到链，当该元素存在与散列表中才删除。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    public void remove(E e) {
        // 获取待删除元素所在链
        LinkedList<E> link = this.lls[hash(e)];
        int index = link.indexOf(e);
        if (index != -1) {
            link.remove(index);
            this.currentSize--;
        }
    }

    扩展

在此列举若干常用的散列表实现：

  • 基于开放定址法的实现

    开放定址法下另有多种实现，分别为基于线性探测法的实现、基于平方探测法的实现和基于双散列的实现。

    • 基于线性探测法的实现

      当发生冲突时，依次探测空间 $h_i(x) = (hash(x) + f(i)) \ %\ tableSize$，如果某个空间未使用，则将元素置于该空间之中，停止探测。

      此方法的一大问题在于将会导致存在 “一次聚集” ，即空间成块使用。

    • 基于平方探测法的实现

      当发生冲突时，依次探测空间 $h_i(x) = (hash(x) + f(i^2)) \ %\ tableSize$，如果某个空间未使用，则将元素置于该空间之中，停止探测。

      此方法可解决 “一次聚集”，但会导致 “二次聚集”。

    • 基于双散列的实现

      当发生冲突时，依次探测空间 $h_i(x) = (i \times hash_2(x)) \ %\ tableSize$，如果某个空间未使用，则将元素置于该空间之中，停止探测。

      如果第二个散列函数选择的好，则散列表性能就好；否则就是灭顶之灾。

  • 再散列

    如果散列表中存在元素过多，则创建一个具有原散列表两倍空间的新散列表，并基于新的散列函数将原散列表中元素映射到新散列表之中。此举的时间复杂度为 $O(N)$，由于不是经常发生此种情况，因此实际效果还行。