数据结构-左式堆

发表于 2020-05-25 分类于数据结构与算法

本文字数： 4.1k 阅读时长 ≈ 4 分钟

概述

左式堆 属于一种特殊的堆。除具有二叉堆所有功能外，它还可以在 $O(log^N)$ 时间复杂度内实现堆合并操作。

其结构图大致如下：

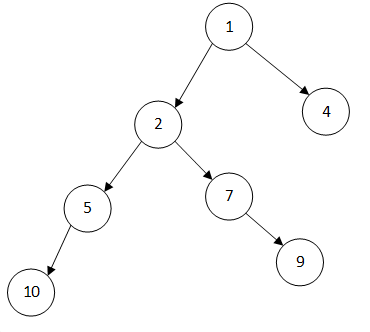
图一：左式堆

左式堆主要涉及一个概念和一个定理，在此先行解释。

零路径长 ($npl(x)$)

节点 $x$ 的零路径长 $npl(x)$ 定义为：从 $x$ 到一个不具有两个儿子节点的最短路径的长。

如果节点 $x$ 具有 0 或 1 个儿子节点，那么 $npl(x) = 0$；如果该节点为空节点，则 $npl(null) = -1$。

根据如上定义，可以推知：任一节点的零路径长比它的各个儿子节点的零路径长的最小值大一。

此时可以给出左式堆的具体定义：左式堆是一棵具有堆序性质的二叉树，而且对于堆中任一节点而言，其左儿子节点的零路径长总是大于等于右儿子节点的零路径长。
在右路径上有 $r$ 个节点的左式堆必然至少有 $2^r -1$ 个节点。

右路径：左式堆最右侧节点所形成的的路径。

使用数学归纳法加以证明。

如果 $i = 1$，左式堆具有 $1$ 个节点，符合定理。

假定 $i = r$ 符合定理。当 $i = r + 1$ 时，可知右子堆至少具有 $2^r - 1$ 个节点，为满足 “左儿子节点的零路径长总是大于等于右儿子节点的零路径长”，可知左子堆同样至少具有 $2^r - 1$ 个节点，再加上一个根节点，总的节点个数至少为 $(2^r - 1) * 2 + 1 = 2^{r + 1} - 1$，符合定理。故而证明完毕。

该定理没有什么用，我们主要使用它的推导定理：具有 $N$ 个节点的左式堆，其右路径最多含有 $log^{N + 1}$ 节点。

由于右路径具有这样的性质，所以我们将对左式堆的所有操作都放到右路径上进行。这样也保证了复杂度为 $O(log^N)$。

结构

左式堆中元素需可比较，为简化代码，我们直接在内部存储一个比较类，用于比较堆中元素。另外节点结构除保存元素外，还需保存 $npl$。

class LeftHeap<E> {
    // 节点结构
    private static class Node<E> {
        // 具体元素
        E item;
        // 左儿子
        Node<E> left;
        // 右儿子
        Node<E> right;
        // 零路径长
        int npl;

        public Node(E item, Node<E> left, Node<E> right, int npl) {
            this.item = item;
            this.left = left;
            this.right = right;
            this.npl = npl;
        }
    }
    // 比较函数
    private final Comparator<? super E> comparator;
    // 根节点
    private Node<E> root;
}

实现

辅助方法

$npl(x)$

1
2
3

private int npl(Node<E> e) {
    return null == e ? -1 : e.npl;
}

合并

对链式结构的操作，基于递归实现往往比较简单。因此在此虽同时给出递归和迭代思路，但是仅给出递归代码。

基于递归

如果一方为空，则直接返回另一方。
比较两方根节点，合并根节点较大者与根节点较小者的右子树，并将其作为根节点较小者的右子树，做相关调整（包括：是否需交换左右子树以满足 “左儿子节点的零路径长总是大于等于右儿子节点的零路径长”、重新计算根节点的零路径长）使当前合并后的左式堆满足要求，然后返回之。

举例：

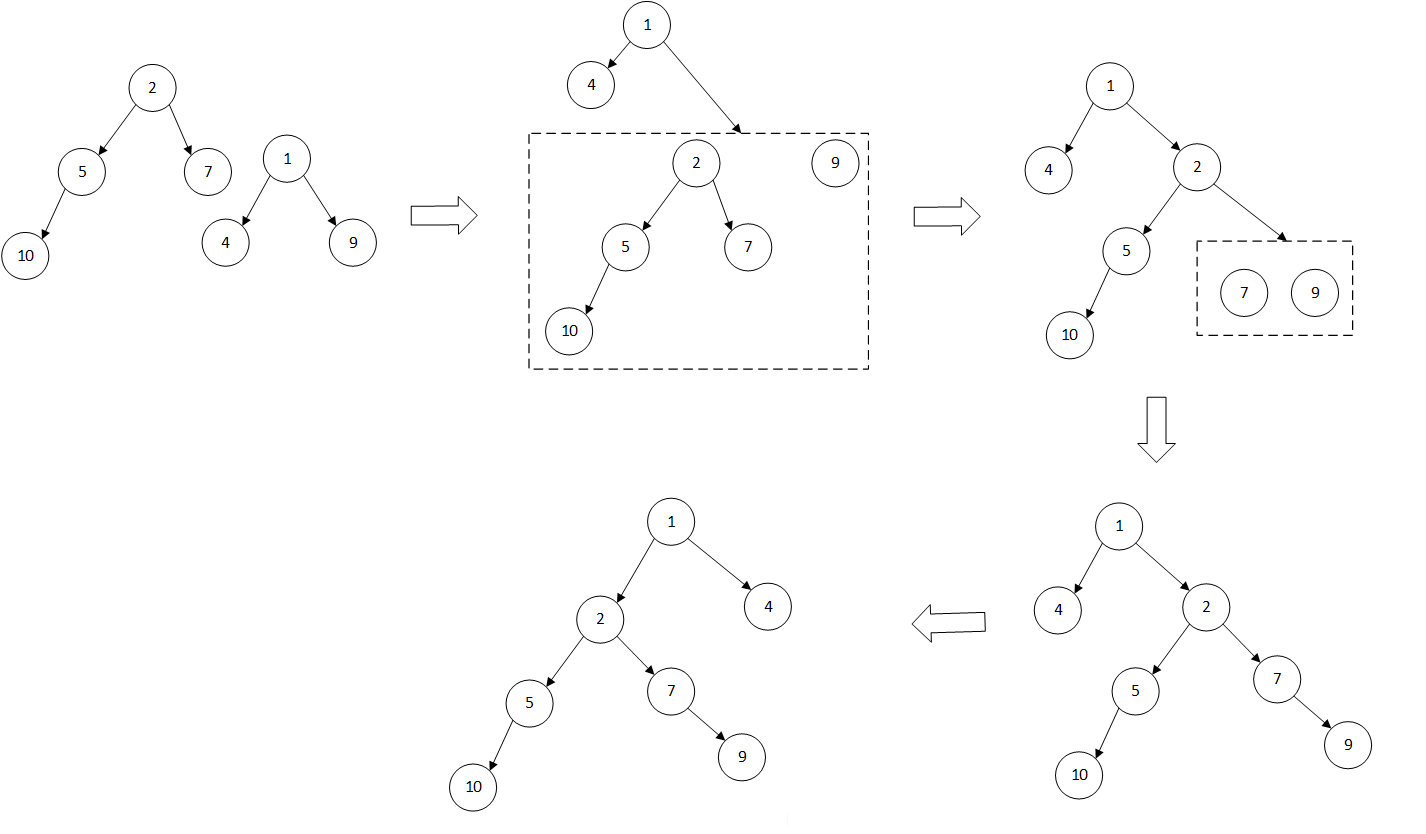
图二：合并左式堆

private Node<E> merge(Node<E> h1, Node<E> h2) {
    // 一方为空，则直接返回另一方
    if (null == h1) {
        return h2;
    }
    if (null == h2) {
        return h1;
    }

    // 二者皆不为空
    // 如果前者根值大于后者根值，需进行交换以保证h1引用根值较小者表示的左式堆。
    if (comparator.compare(h1.item, h2.item) > 0) {
        return merge(h2, h1);
    }

    // 将根值较大者与根值较小者的右子堆合并，合并后的堆成为根值较小者的右子堆，最后调整npl值即可。
    h1.right = merge(h1.right, h2);
    if (npl(h1.left) < npl(h1.right)) {
        // 交换两个节点
        Node<E> tmp = h1.left;
        h1.left = h1.right;
        h1.right = tmp;
    }
    h1.npl = npl(h1.right) + 1;
    return h1;
}

基于迭代

按照大小关系合并两方的右路径以构建一颗新的树。
按照 “左右根” 顺序遍历整棵树，做相关调整（包括：是否需交换左右子树以满足 “左儿子节点的零路径长总是大于等于右儿子节点的零路径长”、重新计算根节点的零路径长），使得此树满足左式堆性质即可。

初始化

1
2
3

public LeftHeap(Comparator<? super E> comparator) {
    this.comparator = comparator;
}

查询

查询最小值

public E getMin() {
    if (null == this.root) {
        return null;
    }
    return this.root.item;
}

操纵

合并两个左式堆

public void merge(LeftHeap<E> leftHeap) {
    if (this == leftHeap) {
        return;
    }
    this.root = merge(this.root, leftHeap.root);
    leftHeap.root = null;
}

堆中添加元素

将待添加元素看做一个左式堆，然后合并两个左式堆即可。

public void insert(E element) {
    Node<E> eNode = new Node<>(element, null, null, 0);
    this.root = merge(this.root, eNode);
}

堆中删除最小元素

删除最小元素，直接合并两个左右子堆即可。

public void deleteMin() {
    if (null == this.root) {
        return ;
    }
    this.root = merge(this.root.left, this.root.right);
}

降低某个节点的元素值

这个操作只提思路，不做实现 (当前左式堆结构无法实现)。

在二叉堆 (小顶堆) 中，这一操作可通过上移至根节点实现，且时间复杂度为 $O(log^N)$。在左式堆中，如果采用相同的实现方法，由于并非所有节点到根节点的距离都是 $O(log^N)$，故而其时间复杂度一定大于 $O(log^N)$。

为保证此操作时间复杂度为 $O(log^N)$，左式堆应当采取另一种实现方法：将该节点与其父节点断开，将形成一个左式堆和一个堆 (可很容易恢复为左式堆)，然后合并二者即可。将堆恢复为左式堆及合并操作的时间复杂度均为 $O(log^N)$，故此操作的时间复杂度亦为 $O(log^N)$。

将堆恢复为左式堆的时间复杂度为 $O(log^N)$，其原因在于：1. 只有父节点到根节点路径上的节点才有可能破坏左式堆性质，因此通过交换左右子树即可恢复性质。2. 由于最大右路径长为 $log^{N + 1}$，故而只需调整从父节点到根结点上的前 $log^{N + 1}$ 个节点即可。
1
public void decreaseKey(Node<E> e, E element) {}
扩展

斜堆是左式堆的自调节形式，它与左式堆的关系类似于伸展树与 AVL 树间的关系。

斜堆本质上只是一个具有堆序的二叉树。相比于左式堆而言，它没有 “其左儿子节点的零路径长总是大于等于右儿子节点的零路径长” 这样的限制，故而关于节点的零路径长信息皆无需保留。也正因如此，斜堆的右路径可以无限长，故而单次操作时间复杂度为 $O(N)$。但是理论证明：对任意 $M$ 次连续操作，总的最坏情形运行时间为 $O(Mlog^N)$，故而平均时间复杂度为 $O(log^N)$。

从左式堆实现中可以看到：其他操纵操纵都是基于合并操作实现的。斜堆亦是如此。故而在此简要介绍斜堆的合并操作。

在斜堆的合并操作中，除右路径最后一个节点外，左右子堆交换总是进行。借助上面合并代码，斜堆的合并代码列举如下：

private Node<E> merge(Node<E> h1, Node<E> h2) {
    // 一方为空，则直接返回另一方
    if (null == h1) {
        return h2;
    }
    if (null == h2) {
        return h1;
    }

    // 二者皆不为空
    // 如果前者根值大于后者根值，需进行交换以保证h1引用根值较小者表示的左式堆。
    if (comparator.compare(h1.item, h2.item) > 0) {
        Node<E> tmp = h1;
        h1 = h2;
        h2 = tmp;
    }

    // 将根值较大者与根值较小者的右子堆合并，合并后的堆成为根值较小者的右子堆。
    h1.right = merge(h1.right, h2);
    // 直接交换两个节点即可，因为h1.right为空情况已在2-8行代码中排除了。
    Node<E> tmp = h1.left;
    h1.left = h1.right;
    h1.right = tmp;
    return h1;
}

概述

结构

实现

辅助方法

初始化

查询

操纵

扩展