数据结构-二项队列

发表于 2020-05-25 分类于数据结构与算法

本文字数： 6.5k 阅读时长 ≈ 6 分钟

概述

二项队列 属于一种构建极为精妙的堆。它不仅具有左式堆的优点（$O(log^N)$ 时间复杂度内实现堆合并），同时具有二叉堆的优点（$O(N)$ 时间复杂度内实现建堆）。

其结构图大致如下：

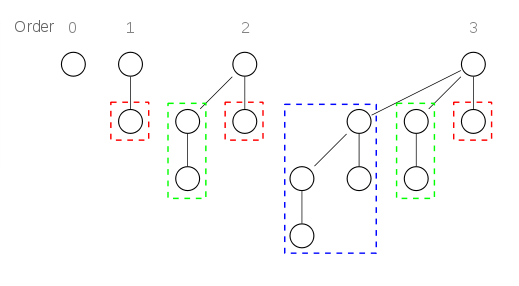
图一：二项队列

二项队列主要涉及一个概念和一个定理，在此先行解释。

二项树 ($B_i$)

高度为 $i$ 的二项树 $B_i$ 构造规则如下：
- 当 $i = 0$ 时，$B_i$ 为一棵单结点树。
- 当 $i > 0$ 时，$B_i$ 通过将一棵二项树 $B_{i - 1}$ 附接到另一棵二项树 $B_{i - 1}$ 的根上而构成。
仔细观察构造规则及上方结构图，我们可得到如下结论：
- 二项树 $B_i$ 由一个带有儿子 $B_0,B_1,\dots,B_{i - 1}$ 的根组成。
- 二项树 $B_i$ 具有 $2^i$ 个结点。
此时可以给出二项队列的具体定义：二项队列是具有堆序结构的二项树的集合，而且该集合中不存在具有相同高度的两棵二项树。
含有 $N$ 个结点的二项队列最多含有 $log^N$ 棵二项树。

此定理证明比较简单。

假定一个二项队列为 ${B_0,B_1,\dots,B_k}$，容易得知其含有 $2^0 + 2^1 + \dots + 2^k = 2^{k + 1} - 1$ 个结点。这句话反过来就是定理。

二项队列的操作都是基于二项树而言的，正是由于具有这样的性质，故而其操作的最坏时间复杂度为 $O(log^N)$。

结构

二项队列结构比较精妙，在此简单说明一下：

二项树具有多个儿子结点，因此我们使用孩子兄弟表示法表示之。
为方便相同高度的二项树合并操作，我们逆向存放子二项树。例如：对于二项树 $B_i$ 而言，其根结点的兄弟结点为 $B_{i - 1}$，$B_{i - 1}$ 的兄弟结点为 $B_{i - 2}$，$\dots$ ，$B_{1}$ 的兄弟结点为 $B_{0}$。
我们采用数组从前往后依次存放相应高度的二项树，这样做的优点在于可以快速获取二项队列中的元素个数，同时方便编写二项队列合并操作的代码。

class BinomialQueue<E> {
    // 孩子兄弟表示法表示一颗二项树
    private static class Node<E> {
        // 具体元素
        E item;
        // 孩子结点
        Node<E> leftChild;
        // 兄弟结点
        Node<E> nextSibling;

        public Node(E item, Node<E> leftChild, Node<E> nextSibling) {
            this.item = item;
            this.leftChild = leftChild;
            this.nextSibling = nextSibling;
        }
    }
    // 二项队列(使用数组保存二项树的根)
    private Node<E>[] trees;
    // 元素个数
    private int currentSize;
    // 比较函数
    private final Comparator<? super E> comparator;
}

实现

辅助方法

扩容

private void expandTrees(int length) {
    Node<E>[] newTrees = new Node[length];
    for (int i = 0; i < this.trees.length; i++) {
        newTrees[i] = this.trees[i];
    }
    this.trees = newTrees;
}

获取最小元素下标

private int findMinIndex() {
    int index = -1;
    E min = null;
    for (int i = 0; i < this.trees.length; i++) {
        if (null == this.trees[i]) {
            continue;
        }
        if (null == min) {
            min = this.trees[i].item;
            index = i;
        } else {
            if (comparator.compare(min, this.trees[i].item) > 0) {
                System.out.println(min + " " + this.trees[i].item);
                min = this.trees[i].item;
                index = i;
            }
        }
    }
    return index;
}

合并高度相同的二项树

如上所述，二项树构造具有一定之规。另外二项队列中的二项树同时需要满足堆序性质。综合二者，二项队列中的二项树合成规则为：$B_i$ 通过将根值较小者/较大者的二项树 $B_{i - 1}$ 附接到另一棵二项树 $B_{i - 1}$ 的根上而构成。

此函数实现代码体现了 “逆向存放子二项树” 的好处。如果顺序存放子二项树，我们应当首先找到 t1.leftChild 的最后一个兄弟结点，然后将其兄弟结点的引用指向 t2。

private Node<E> combineTrees(Node<E> t1, Node<E> t2) {
    if (comparator.compare(t1.item, t2.item) > 0) {
        return combineTrees(t2, t1);
    }
    t2.nextSibling = t1.leftChild;
    t1.leftChild = t2;
    return t1;
}

初始化

空初始化

public BinomialQueue(Comparator<? super E> comparator) {
    this.trees = new Node[1];
    this.comparator = comparator;
}

初始化携带一个元素

public BinomialQueue(Comparator<? super E> comparator, E element) {
    this.trees = new Node[1];
    this.trees[0] = new Node<>(element, null, null);
    this.currentSize = 1;
    this.comparator = comparator;
}

查询

查询容量

1
2
3

public int capacity() {
    return (1 << trees.length) - 1;
}

查询最小值

public E getMin() {
    int index = findMinIndex();
    return index == -1 ? null : this.trees[index].item;
}

操纵

合并两个二项队列

二项队列合并过程类似于数值相加。另外

举例如下：

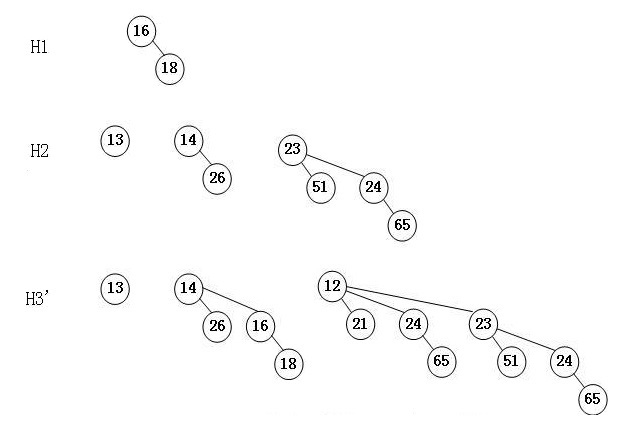
图二：合并二项队列

现需要将 $H1 = {B_1}$ 和 $H2 = {B_0,B_1,B_2}$ 合并为 $H3$ ，具体合并步骤如下：

对于 $H3$ 中的 $B_0$ 而言，$H1$ 没有而 $H2$ 有，则直接将 $H2$ 中的 $B_0$ 赋值给 $H3$ 的 $B_0$ 即可。
对于 $H3$ 中的 $B_1$ 而言，$H1$ 和 $H2$ 均有，合并二者得到 “进位” $B_2$。再无多余 $B_1$，故而 $H3$ 的 $B_1$ 为 $null$。
对于 $H3$ 中的 $B_2$ 而言，$H1$ 没有而$H2$ 有，同时存在一个 “进位” $B_2$，合并二者得到 “进位” $B_3$。再无多余 $B_2$，故而 $H3$ 的 $B_2$ 为 $null$。
对于 $H3$ 中的 $B_3$ 而言，$H1$ 和 $H2$ 均无，但是存在一个 “进位” $B_3$，直接将进位$B_3$赋值给$H3$ 的 $B_3$ 即可。
$H1$ 和 $H2$ 无再合并之物，则合并结果为 $H3 = {B_0,B_2,B_3}$。

public void merge(BinomialQueue<E> binomialQueue) {
    if (this == binomialQueue) {
        return ;
    }
    this.currentSize += binomialQueue.currentSize;
    //空间不足，需要扩容。这是一种扩容方式。
    if (this.currentSize > capacity()) {
        int maxLength = Math.max(this.trees.length, binomialQueue.trees.length);
        expandTrees(maxLength + 1);
    }

    // 保存上一次合并结果的“余数”
    Node<E> carry = null;
    for (int i = 0; i < this.trees.length; i++) {
        Node<E> t1 = this.trees[i];
        Node<E> t2 = i < binomialQueue.trees.length ? binomialQueue.trees[i] : null;

        int whichCase = t1 == null ? 0 : 1;
        whichCase += t2 == null ? 0 : 2;
        whichCase += carry == null ? 0 : 4;

        switch (whichCase) {
            // 表明t2和carry均为null，无需操作
            case 0:
            case 1:
                break;
            // 表明仅t2不为空，直接赋给this即可
            case 2:
                this.trees[i] = t2;
                binomialQueue.trees[i] = null;
                break;
            // 表明t1和t2均不为空，合并即可。
            case 3:
                carry = combineTrees(t1, t2);
                this.trees[i] = binomialQueue.trees[i] = null;
                break;
            // 表明仅carry不为空，直接赋给this即可
            case 4:
                this.trees[i] = carry;
                carry = null;
                break;
            // 表明仅t1和carry不为空，合并即可
            case 5:
                carry = combineTrees(t1, carry);
                this.trees[i] = null;
                break;
            // 表明仅t2和carry不为空，合并即可
            case 6:
                carry = combineTrees(t2, carry);
                binomialQueue.trees[i] = null;
                break;
            // 表明三者俱在
            case 7:
                carry = combineTrees(t2, carry);
                binomialQueue.trees[i] = null;
                break;
        }
    }

    // 调整待合并堆相关参数
    binomialQueue.currentSize = 0;
}

二项队列中添加元素

将待添加元素看做一个二项队列，合并二者即可。
1
2
3
4
public void insert(E element) {
BinomialQueue<E> eBinomialQueue = new BinomialQueue<>(this.comparator, element);
merge(eBinomialQueue);
}
此处我们分析一下为什么可在 $O(N)$ 时间复杂度内实现建堆？也即为什么插入操作的平均时间复杂度为 $O(1)$ ？

通过上面的合并代码，可以发现合并两个二项队列所花费的时间依托于其上的二项树分布。
- 如果将仅含一个元素的二项队列与一个含有偶数个元素的二项队列合并，仅需合并到 $B_0$ 即可，故而花费时间为 O(1)。
- 如果将仅含一个元素的二项队列与含有 $2^k - 1$ 个元素的二项队列合并，由于已有 $B_0,B_1,\dots, B_{k-1}$，所以需一直合并到 $B_k$，故而花费时间为 $O(k)$。
上述两种情况属于运行时间的最好情况和最坏情况。最好情况的发生概率为 $1/2$，最坏情况的发生概率则极低。

假定总共执行插入操作 $N$ 次，可粗略得到：$N/2$ 次插入的运行时间为 $O(1)$，$N / 4$ 次插入的运行时间为 $O(2)$，$\dots$，$N/2^k$ 次插入的运行时间为 $O(k)$。

所有 $N$ 次插入的总运行时间为：$\sum_{i = 1}^k\frac{N \times i}{2^i} < N \times \sum_{i = 1}^\infty\frac{i}{2^i} = 2N$。

故而一次插入操作的平均运行时间为 $2N / N = 2 = O(1)$，所以可在 $O(N)$ 时间复杂度内实现建堆。

二项队列中删除最小元素

最小元素一定属于某个二项树的根结点。首先从当前二项队列中删除此二项树，然后使用该二项树的子二项树构建一个二项队列，合并此二者即可达到 “从二项队列中删除最小元素” 的目的。

public E deleteMin() {
    // 为空则直接返回
    if (this.currentSize == 0) {
        return null;
    }

    int index = findMinIndex();
    E minElement = this.trees[index].item;
    Node<E> deletedTree = this.trees[index].leftChild;

    // 基于该二项队列的子二项树构建一个二项队列。
    BinomialQueue eBinomialQueue = new BinomialQueue(this.comparator);
    eBinomialQueue.expandTrees(index);
    for (int i = index - 1; i >= 0; i--) {
        eBinomialQueue.trees[i] = deletedTree;
        deletedTree = deletedTree.nextSibling;
        eBinomialQueue.trees[i].nextSibling = null;
    }
    eBinomialQueue.currentSize += ((1 << index) - 1);

    this.trees[index] = null;
    this.currentSize -= (1 << index);

    merge(eBinomialQueue);
    return minElement;
}

拓展

为进一步降低二项队列相关操作的时间复杂度，懒惰二项队列 应运而生，它通过支持懒惰合并使得合并操作的

平均时间复杂度为 $O(1)$，同时保证删除最小元素操作的平均时间复杂度仍为 $O(log^N)$。

由于支持懒惰合并，因此懒惰二项队列的具体定义如下：懒惰二项队列是具有堆序结构的二项树的集合，它允许集合中存在高度相同的两棵二项树。

懒惰合并仅涉及合并操作和删除最小元素操作，因此在此详述二者。

合并操作

直接将高度相同的二项树放在一起即可。
删除最小元素操作

遍历所有二项树，找到最小元素将其删除。随后我们需要将懒惰二项队列转变为标准的二项队列，即通过合并二项树，使得集合中不存在高度相同的两棵二项树。

合并操作和删除最小元素的平均时间复杂度证明过程极为复杂，这里省略。

为支持懒惰二项队列，将二项队列结构中的 private Node<E>[] trees; 修改为 private LinkedList<Node<E>> trees 即可得到懒惰二项队列结构。

通过合并操作和删除最小元素操作的具体内容，可以得知：懒惰合并指代只有当两个二项队列真正需要合并时 (即删除最小元素后) 才进行合并。