数据结构-二叉堆

发表于 2020-05-22 分类于数据结构与算法

本文字数： 4.3k 阅读时长 ≈ 4 分钟

概述

二叉堆 属于一种特殊的堆，其本质为一颗完全二叉树。

二叉堆分为两种——大顶堆和小顶堆。二者结构图大致如下：

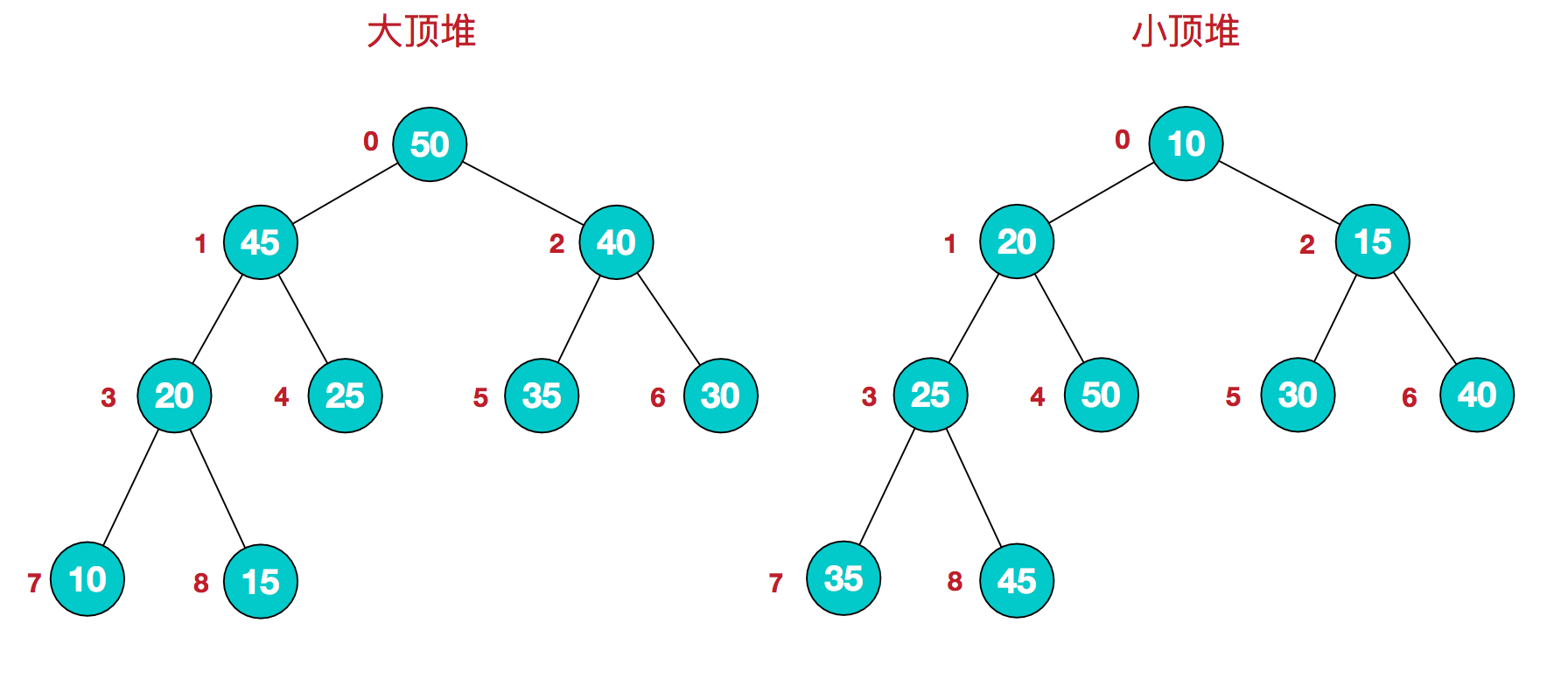
图一：二叉堆

二叉堆本质上是一棵二叉树，通常应当采用链式存储结构加以实现。由于完全二叉树的性质，我们可以很方便地使用数组实现二叉堆。另外大顶堆与小顶堆原理相同，实现也差不多。故而，本文基于数组实现一个小顶堆。

结构

堆中元素需可比较，为简化代码，我们直接在内部存储一个比较类，用于比较堆中元素。

class BinaryHeap<E> {
    // 比较函数
    private final Comparator<? super E> comparator;
    // 基础数组(从下标1开始存储元素)
    private Object[] elementData;
    // 元素个数
    private int size;
}

实现

对堆进行操作后，需保持堆性质 (每个结点表示值总是大于/小于左右子结点表示值) 不发生变化。

辅助方法

堆具有两大基本操作——上移和下沉。

上移

将指定位置结点上移时，将首先判断当前结点与父结点间大小关系。如果当前结点较小，则需将二者交换然后进一步判断父结点，反之表明已符合堆性质，直接退出即可。

// 迭代写法
public void up(int index) {
    final int length = this.size;
    final Object element = this.elementData[index];

    for (int i = index / 2; i > 0; i = i / 2) {
        if (comparator.compare((E) this.elementData[i], (E) element) > 0) {
            this.elementData[index] = this.elementData[i];
            index = i;
        } else {
            break;
        }
    }
    this.elementData[index] = element;
}

// 递归写法
// 将element上移到堆中合适的位置，现已处理到index
public void upD(Object element, int index) {
    if (index / 2 <= 0) {
        this.elementData[index] = element;
        return ;
    }
    int i = index / 2;
    if (comparator.compare((E) this.elementData[i], (E) element) > 0) {
        this.elementData[index] = this.elementData[i];
        index = i;
        upD(element, index);
    } else {
        this.elementData[index] = element;
    }
}

下沉

将指定位置结点下沉时，将首先判断当前结点与左右子结点较小者间大小关系。如果当前结点较大，则需将二者交换然后进一步判断左右子结点较小者，反之表明已符合堆性质，直接退出即可。

// 迭代写法
public void down(int index) {
    final int length = this.size;
    final Object element = this.elementData[index];
    for (int i = index * 2; i <= length; i = i * 2) {
        // 找寻左右儿子中小者
        if (i < length && comparator.compare((E) this.elementData[i], (E) this.elementData[i + 1]) > 0) {
            i = i + 1;
        }
        if (comparator.compare((E) this.elementData[i], (E) element) < 0) {
            this.elementData[index] = this.elementData[i];
            index = i;
        } else {
            break;
        }
    }
    this.elementData[index] = element;
}

// 递归写法
// 将element下沉到堆中合适的位置，现已处理到index
public void downD(Object element, int index) {
    if (index * 2 > this.size) {
        this.elementData[index] = element;
        return ;
    } else {
        int i = index * 2;
        if (i < this.size && comparator.compare((E) this.elementData[i], (E) this.elementData[i + 1]) > 0) {
            i = i + 1;
        }
        if (comparator.compare((E) this.elementData[i], (E) element) < 0) {
            this.elementData[index] = this.elementData[i];
            index = i;
            downD(element, index);
        } else {
            this.elementData[index] = element;
        }
    }
}

描述性内容写的是 “交换两个结点”；但是代码实现中略有不同。原因如下：假定执行一次上移共需迭代 $d$ 次。对于前者需执行 $3d$ 次赋值操作，而后者则仅需要 $d + 1$ 次赋值。

使用前者带来的负担是：运行效率略低；使用后者带来的负担则是：递归写法比较复杂。

初始化

堆初始化存在两种方式——自顶向下和自底向上。前者复杂度为 $O(Nlog^N)$，后者复杂度为 $O(N)$。

自顶向下初始化

此种初始化方式比较简单，就是将每个元素依次插入到堆中即可。

public BinaryHeap(E [] arr, Comparator<? super E> comparator) {
    final int length = arr.length;
    this.comparator = comparator;
    this.elementData = new Object[100];
    for (int i = 0;i < length; i++) {
        insert(arr[i]);
    }
}

复杂度分析

容易知道，插入元素的时间复杂度为 $O(log^N)$ ，其中 $N$ 为当前堆中结点个数。

那么自顶向下初始化过程的时间复杂度便是：$\sum_{i = 1}^Nlog^i$，其中 $N$ 为最终堆中结点个数。

基于积分学知识，我们知道：$\int_{i - 1}^ilog^idi < log^i < \int_i^{i + 1}log^idi$，那么便有如下等式：

$$\sum_{i = 1}^N(\int_{i - 1}^ilog^idi) < \sum_{i = 1}^Nlog^i < \sum_{i = 1}^N\int_i^{i + 1}log^idi$$

$$\int_0^Nlog^idi < \sum_{i = 1}^Nlog^i < \int_1^{N + 1}log^idi$$

左右两端结果均为 $O(Nlog^N)$，故而 $\sum_{i = 1}^Nlog^i \approx O(Nlog^N)$。

所以，自顶向下初始化过程的时间复杂度为 $O(Nlog^N)$。

自底向上初始化

此种初始化方式比较巧妙，将非叶结点依次下沉即可得到一个堆。

public BinaryHeap(Comparator<? super E> comparator, E [] arr) {
    final int length = arr.length;
    this.comparator = comparator;
    this.elementData = new Object[100];
    this.size = length;
    for (int i = 0; i < length; i++) {
        this.elementData[i + 1] = arr[i];
    }
    for (int i = length / 2; i > 0; i--) {
        down(i);
    }
}

容易知道，下沉结点的时间复杂度为 $O(log^h)$，其中 $h$ 为当前结点的高度。

那么自底向上初始化过程的时间复杂度便是所有结点的高度之和，即 $S = \sum_{i = 0}^h2^i\times (h - i)$，其中 $h$ 为最终堆的高度。

使用错位相减法求解该式，可以得到 $S \approx O(2^h)$。高度为 $h$ 的完全二叉树，其结点个数 $N$ 满足等式 $2^h < N < 2^{h + 1}$，故而 $S \approx O(N)$。

所以，自底向上初始化过程的时间复杂度为 $O(N)$。

查询

查询最小值

1
2
3

public E getMin() {
    return this.size == 0 ? null : (E) this.elementData[1];
}

操纵

堆中添加元素

方法十分巧妙。将待添加元素置于堆末，然后上移该结点，即可实现将元素添加到堆中。
1
2
3
4
public void insert(E element) {
this.elementData[++this.size] = element;
up(this.size);
}

堆中删除最小元素

方法十分巧妙。将堆头结点与堆末结点互换，此时删除堆末结点十分简单，然后下沉堆头结点，即可实现将最小元素从堆中删除。

public E deleteMin() {
    if (this.size <= 0)
        return null;
    E element = (E) this.elementData[1];
    if (this.size == 1) {
        this.size--;
        return element;
    } else {
        this.elementData[1] = this.elementData[this.size--];
        down(1);
        return element;
    }
}