数据结构-队列/栈

发表于 分类于
本文字数： 4.1k 阅读时长 ≈ 4 分钟

概述

队列 属于一种特殊的线性表/链表，它仅允许从一端插入元素、另一端删除元素。

栈 属于一种特殊的线性表/链表，它仅允许在某一端插入、删除元素。

其结构图大致如下：

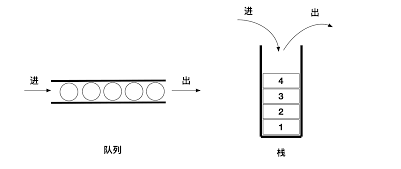
图一：队列/栈

我们并不单独实现队列/栈，而是仅实现一个双端队列，它不仅具有队列功能、也具有栈功能。

双端队列实现方法有两种，一种基于循环数组，另一种基于链表。基于链表的已在 数据结构-链表 中给出，故而此处的双端队列基于循环数组实现。

结构

在 Java 库中，ArrayDeque 类为双端队列的实现。在这种实现方法中，其中无法存储 null 值。

我们采用 Java库中类似方法，并在稍后代码中给出无法存储 null 值的原因。

1
2
3
4
5
6
7
8
9
10
class ArrayDeque<E> {
    // 默认容量
    private static final int DEFAULT_CAPACITY = 16;
    // 基础数组
    private Object[] elementData;
    // 队首(指向第一个元素的位置)
    private int head;
    // 队尾(指向最后一个元素的下一个位置)
    private int tail;
}

实现

辅助方法

  • 单增($0 \leq i < modulus$)

    1
    2
    3
    4
    5
    6
    private int inc(int i, int modulus) {
        if ((++i) >= modulus) {
            i = 0;
        }
        return i;
    }

  • 多增

    1
    2
    3
    4
    5
    6
    private int inc(int i, int distance, int modulus) {
        if((i += distance) >= modulus) {
            i -= modulus;
        }
        return i;
    }

  • 单减($0 \leq i < modulus$)

    1
    2
    3
    4
    5
    6
    private int dec(int i, int modulus) {
        if ((--i) < 0) {
            i = modulus - 1;
        }
        return i;
    }

  • 多减

    1
    2
    3
    4
    5
    6
    private int sub(int i, int j, int modulus) {
        if ((i -= j) < 0) {
            i += modulus;
        }
        return i;
    }

  • 扩容

    第 9 行代码可以看到，它借用 null 判断该双端队列为满状态还是空状态。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    private void grow() {
        int oldCapacity = this.elementData.length;
        Object[] elementData = new Object[oldCapacity + (oldCapacity >> 1)];
        // 将全部元素赋值过去
        for (int i = 0; i < oldCapacity; i++) {
            elementData[i] = this.elementData[i];
        }
        // 将原数组中右半部分元素移动到新数组中右半部分。
        if (this.tail < this.head || (this.tail == this.head && null !=this.elementData[this.head])) {
            int spaceCapacity = oldCapacity >> 1;
            for (int i = this.head; i < oldCapacity; i++) {
                elementData[i + spaceCapacity] = this.elementData[i];
            }
            this.head += spaceCapacity;
        }
        this.elementData = elementData;
    }

    单增、多增、单减、多减四个函数意在封装下标移动时的取模操作。

初始化

  • 空初始化

    1
    2
    3
    public ArrayDeque() {
        this(ArrayDeque.DEFAULT_CAPACITY);
    }

  • 带参数初始化

    1
    2
    3
    4
    5
    public ArrayDeque(int initialCapacity) {
        if (initialCapacity < 0)
            initialCapacity = 0;
        this.elementData = new Object[initialCapacity + 1];
    }

    查询

  • 查询元素个数

    我们无需变量存放元素个数信息，只需通过队首、队尾相减即可得到该信息。

    1
    2
    3
    public int size() {
        return sub(this.tail, this.head, this.elementData.length);
    }

  • 查询双端队列是否为空

    1
    2
    3
    public boolean isEmpty() {
            return size() == 0;
    }

  • 查询队首

    1
    2
    3
    4
    5
    6
    7
    8
    // ArrayDequeu中二者是有差别的。如果双端队列为空，前者返回一个异常，后者返回null。对此我做了简化。
    public E getFirst() {
        return (E) this.elementData[this.head];
    }

    public E peekFirst() {
        return getFirst();
    }

  • 查询队尾

    1
    2
    3
    4
    5
    6
    7
    8
    // ArrayDequeu中二者是有差别的。如果双端队列为空，前者返回一个异常，后者返回null。对此我做了简化。
    public E getLast() {
        return (E) this.elementData[dec(this.tail, this.elementData.length)];
    }

    public E peekLast() {
        return getLast();
    }

    操纵

  • 队首添加元素

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    // ArrayDequeu中二者是有差别的。如果双端队列为空，前者返回一个异常，后者返回null。对此我做了简化。
    public void addFirst(E e) {
        if (null == e) {
            return;
        }
        this.elementData[this.head = dec(this.head,this.elementData.length)] = e;
        if (this.head == this.tail) {
            grow();
        }
    }

    public boolean offerFirst(E e) {
        addFirst(e);
        return true;
    }

  • 队尾添加元素

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    // ArrayDequeu中二者是有差别的。如果双端队列为空，前者返回一个异常，后者返回null。对此我做了简化。
    public void addLast(E e) {
        if (null == e) {
            return ;
        }
        this.elementData[this.tail] = e;
        this.tail = inc(this.tail,this.elementData.length);
        if (this.head == this.tail) {
            grow();
        }
    }

    public boolean offerLast(E e) {
        addLast(e);
        return true;
    }

  • 队首删除元素

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    // ArrayDequeu中二者是有差别的。如果双端队列为空，前者返回一个异常，后者返回null。对此我做了简化。
    public E removeFirst() {
        final E e = (E) this.elementData[this.head];
        if (null != e) {
            this.elementData[this.head] = null;
            this.head = inc(this.head, this.elementData.length);
        }
        return e;
    }

    public E pollFirst() {
        return removeFirst();
    }

  • 队尾删除元素

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    // ArrayDequeu中二者是有差别的。如果双端队列为空，前者返回一个异常，后者返回null。对此我做了简化。
    public E removeLast() {
        final int index = dec(this.tail, this.elementData.length);
        final E e = (E) this.elementData[index];
        if (null != e) {
            this.elementData[index] = null;
            this.tail = index;
        }
        return e;
    }

    public E pollLast() {
        return removeLast();
    }

  • 清空双端队列

    1
    2
    3
    4
    5
    6
    7
    public void clear() {
        for (int i = this.head; i != this.tail; i = inc(i, this.elementData.length)) {
            this.elementData[i] = null;
        }
        this.head = 0;
        this.tail = 0;
    }

扩展

对队列/栈中元素施加以单调性质便形成了一种新的数据结构——单调队列/单调栈。在单调队列/单调栈中，所有元素按序单调递增或单调递增。

该种数据结构用途不太广泛，仅能处理一种特定问题—— Next Greater Element。例如：给你一个数组，返回一个等长的数组，对应索引存储着下一个更大元素，如果没有更大的元素，就存 -1。如果输入为 [2,1,2,4,3] ，输出应当为 [4,2,4,-1,-1] 。基于单调栈，从后往前存储数组元素即可解决此问题。