数据结构-线性表

发表于 分类于
本文字数： 2.7k 阅读时长 ≈ 2 分钟

概述

线性表 是具有线性结构特点、最简单、且最常用的一种数据结构。它是具有相同特性的数据元素组成的一个有限序列。

其结构图大致如下：

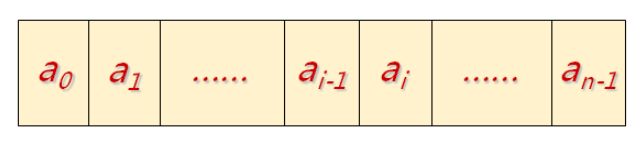
图一：线性表

线性表的优缺点：

  • 优点
    1. 随机存取。
    2. 无需额外空间保存元素间逻辑关系。
  • 缺点
    1. 插入、删除需要移动大量元素。
    2. 可能存在存储空间“碎片“，即申请了但未使用的空间。

结构

线性表需要先申请一定空间，然后再想其中存放元素，因此存在 容量 和 元素个数 两个概念。其中 容量 指的是当前线性表可容纳的元素个数；元素个数 指的是当前线性表已容纳的元素个数。由于 Java 数组本身就保存容量信息，因此在此无需存储它，仅需存储元素个数即可。

1
2
3
4
5
6
7
8
class ArrayList<E> {
    // 默认容量
    private static final int DEFAULT_CAPACITY = 10;
    // 基础数组
    private Object[] elementData;
    // 元素个数
    private int size;
}

实现

辅助方法

  • 扩容

    每扩充一次，线性表容量增加一半。

    1
    2
    3
    4
    5
    6
    private Object[] grow() {
        Object[] newElementData = new Object[this.elementData.length + (this.elementData.length >> 1)];
        for (int i = 0;i < this.size; i++)
            newElementData[i] = this.elementData[i];
        return newElementData;
    }

    初始化

  • 空初始化

    1
    2
    3
    public ArrayList() {
        this(ArrayList.DEFAULT_CAPACITY);
    }

  • 带参数初始化

    1
    2
    3
    4
    5
    public ArrayList(int initialCapacity) {
        if (initialCapacity < 0)
            initialCapacity = 0;
        this.elementData = new Object[initialCapacity];
    }

    查询

  • 查询元素个数

    1
    2
    3
    public int size() {
        return this.size;
    }

  • 查询线性表是否为空

    1
    2
    3
    public boolean isEmpty() {
        return size() == 0;
    }

  • 查询元素位置

    如果存在则返回其下标，否则返回 -1。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    public int indexOf(Object o) {
        if (null == o)  {
            for (int i = 0; i < this.size; i++) {
                if (null == this.elementData[i])
                    return i;
            }
        } else {
            for (int i = 0; i < this.size; i++) {
                if (o.equals(this.elementData[i]))
                    return i;
            }
        }
        return -1;
    }

  • 查询指定位置内容

    1
    2
    3
    4
    5
    6
    7
    public E get(int index) {
        if (index < 0 || index >= this.size) {
            return null;
        } else {
            return (E)this.elementData[index];
        }
    }

    操纵

  • 指定位置添加元素

    添加元素之前需要判断容量是否足够，不够则扩容。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    public boolean add(int index, E element) {
        if (index < 0 || index > this.size) {
            return false;
        } else {
            if (this.elementData.length == this.size) {
                this.elementData = grow();
            }
            for (int i = this.size; i >= index; i--)
                this.elementData[i + 1] = this.elementData[i];
            this.elementData[index] = element;
            this.size = this.size + 1;
            return true;
        }
    }

  • 线性表末添加元素

    1
    2
    3
    public boolean add(E element) {
        return add(size(),element);
    }

  • 删除指定位置元素

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    public E remove(int index) {
        if(index < 0 || index >= this.size) {
            return null;
        } else {
            E oldElement = (E) this.elementData[index];
            for (int i = index; i < this.size; i++) {
                this.elementData[i + 1] = this.elementData[i];
            }
            this.size = this.size - 1;
            this.elementData[this.size] = null;
            return oldElement;
        }
    }

  • 清空线性表

    1
    2
    3
    4
    5
    public void clear() {
        for (int i = 0; i < this.size; i++)
            this.elementData[i] = null;
        this.size = 0;
    }

  • 修改指定位置元素

    修改指定位置元素并返回旧元素。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    public E set(int index, E element) {
        if (index < 0 || index >= this.size) {
            return null;
        } else {
            E oldElement = (E)this.elementData[index];
            this.elementData[index] = element;
            return oldElement;
        }
    }

扩展

将 “分块思想” 应用于线性表之中，便得到了一种新的数据结构——块状数组。块状数组将首先对整个数组进行分块处理，所有针对数组的操作，将首先施加于分块之上，然后进一步施加于分块所在的块数组之上。

块状数组之上各种操作的时间复杂度均为 $O(\sqrt{N})$，其常用于区间求和、区间查询等问题。

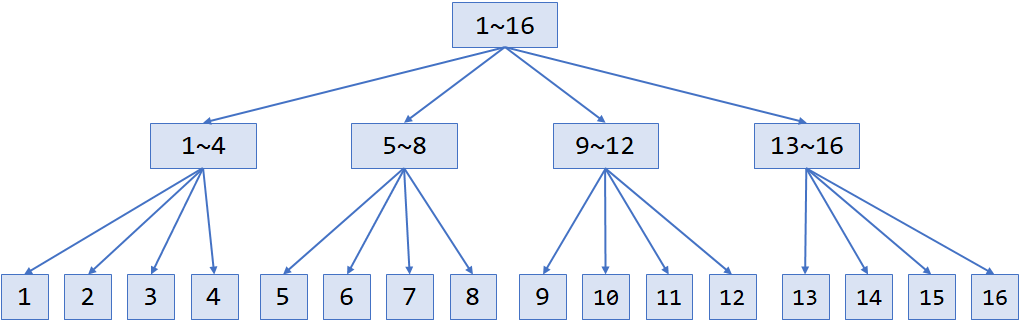
图二：块状数组

块状数组代码实现比较灵活，故而在此简单介绍思想即可。

相关文章